Phasors

Uses Complex Numbers
Phasor Form
$v\left(t\right)=\sqrt{2}V\cos \left(\omega t+\theta \right)$
which can also be represented as
$v\left(t\right)=\mathrm{Re}\left\{\sqrt{2}V{e}^{j\left(\omega t+\theta \right)}\right\}$
Noting that $\sqrt{2}V=V_{peak}$ and that this can also be written in its sinusoidal form.

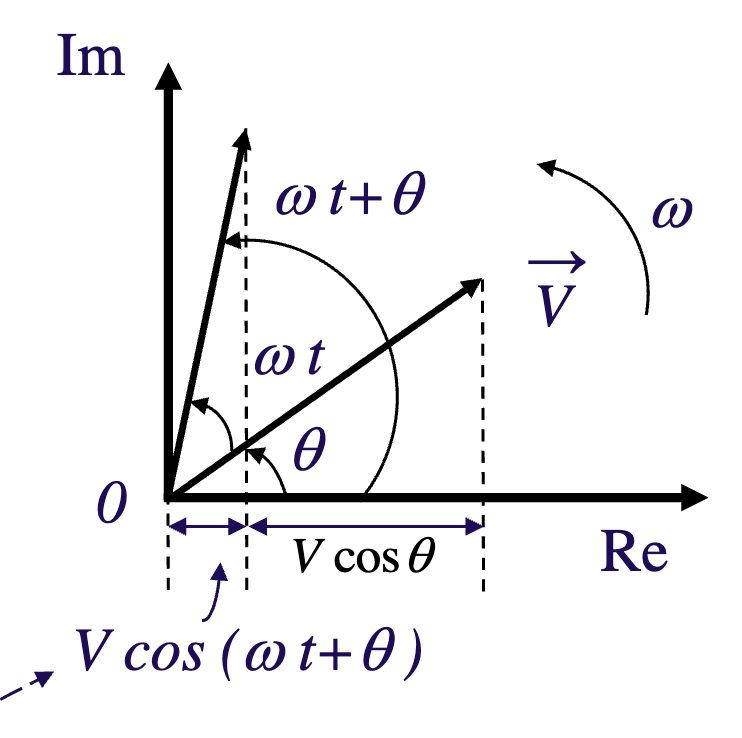
When talking about phasors, we use RMS values.

Voltage and Current Phasor Relationships

$\overrightarrow{V}=Z\overrightarrow{I}$ and also ${\frac{V<\theta v}{I<{\theta }_i}}_{}$

remembering that “dividing” angles is subtraction.
$Z=\left|Z\right|<\varphi =R+jX$
Where Z = Impedance, R = Reactance

Example (Week 1)

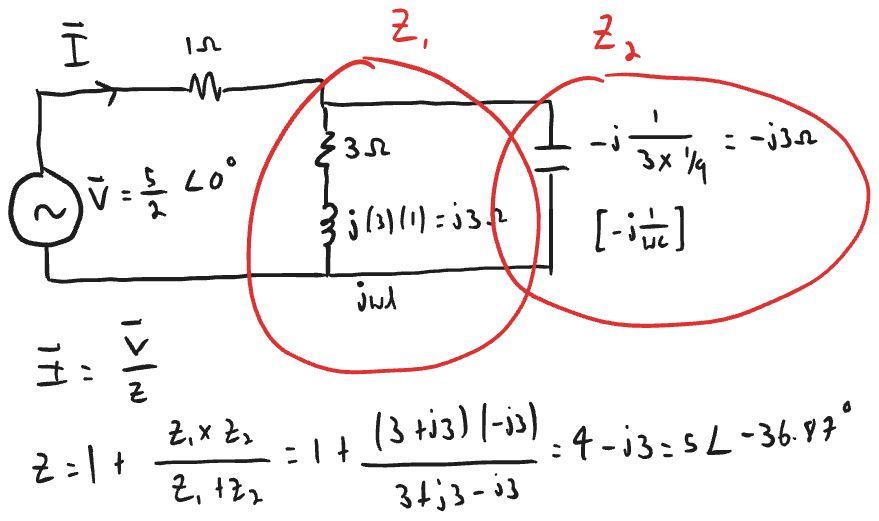
Tips for solving Phasers

• Make use of KVL and KCL (specifically CDR to get branched currents and then V or the other way around (then ohms law))
• Try to use polar form
• the general form of a time expression is $v\left(t\right)=A\sqrt{2}\cos \left(wt-\varphi \right)\left[v\right]$

where the root 2 is to turn the RMS value into a peak value