Deflection and the Elastic Curve

Deflection due to bending

Beams and Springs

The spring force is F=ky where k is some constant.
$k\left(y\right)={\lim }_{\Delta y\to 0}\frac{\Delta F}{\Delta Y}=\frac{df}{dy}$

Deflection

For a uniform bar in pure tension or compression and assuming a linear spring
$\delta =\frac{Fl}{AE}$
$k=\frac{AE}{l}$
For a solid round bar
$k=\frac{GJ}{l}$ and $\theta =\frac{T}{k}$

Deformation under transverse loading

For general transverse loading
$\frac{1}{\rho }=\frac{M\left(x\right)}{EI}$
where curvature varies linearly with x

Maximum Curvature

Concave up = +M Maximum curvature occurs at the maximum moment location An equation for the beam shape or an elastic curve is required to determine maximum deflection and slope

Elastic Curve

$EI\frac{1}{\rho }=EI\frac{d^{2}y}{d{x}^2}=M\left(x\right)$
Where EI is the flexure of rigidity

$EI\theta =EI\frac{dy}{dx}={\int }_0^{x}M\left(x\right)dx+C_1$
$EIy={\int }_0^{x}dx{\int }_0^{x}M\left(x\right)dx+C_1+C_2$
Where the equation above describes deflection at any point once C1 and C2 are found

For the three types of beams, the boundary conditions for these ODEs can be found

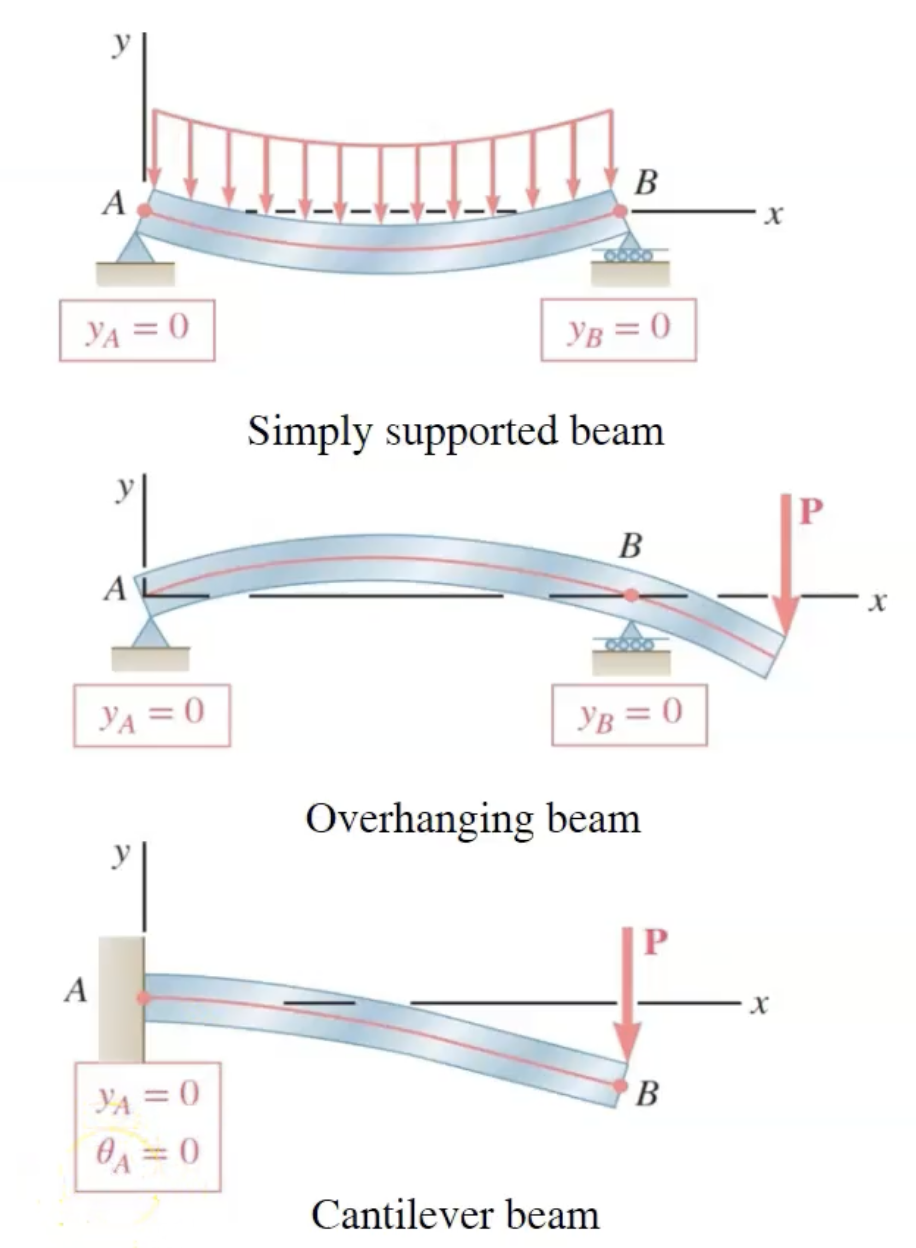
Similar boundary conditions can be determined for a load distribution

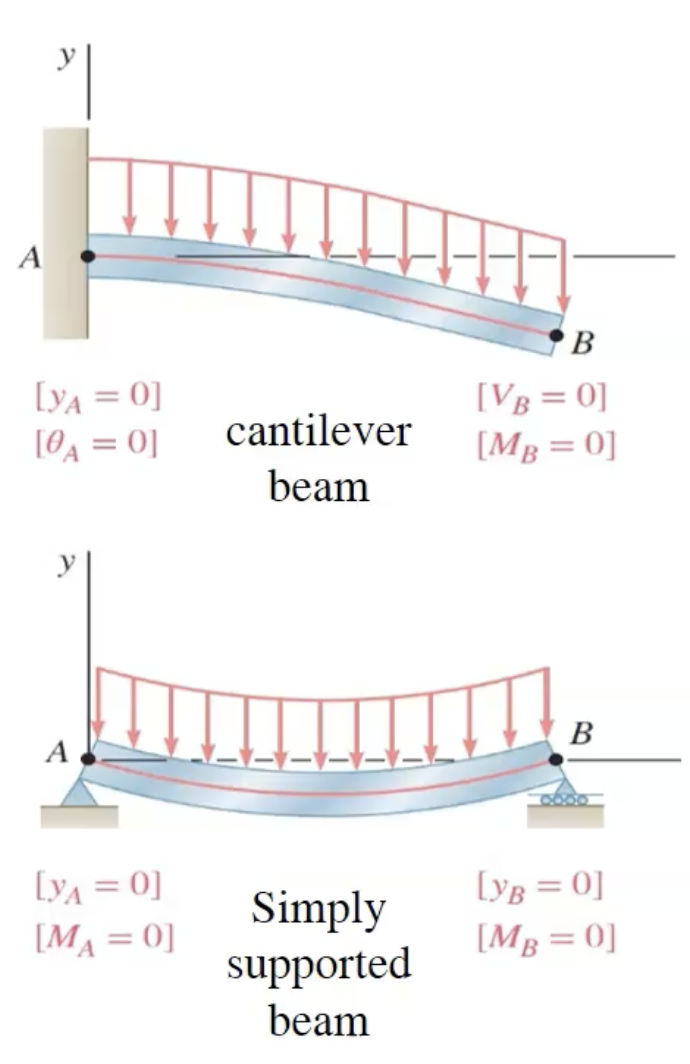
Statically Indeterminate Beams

Where there are more unknowns than equations

For statically indeterminate questions, you can use the beam deflection equation which provides more equations from the boundary conditions.

General Strategy

1. Cut to make a section x away from a support and draw an FBD to get moment equation
2. Develop a DE for the elastic curve
3. Integrate twice
4. Apply boundary conditions to solve for C’s (and other unknowns for a statically indeterminate problem)