The Stress-Life Method and S-N

Summary

Considers empirical data obtained through testing of specimens under controlled cycling between two stress levels

Constant Amplitude Loading

$${\sigma }_{\text{min}}=\text{minimum stress}$$ $${\sigma }_{\text{max}}=\text{maximum stress}$$ $${\sigma }_m=\text{mean (or midrange) stress}=\frac{{\sigma }_{\text{max}}+{\sigma }_{\text{min}}}{2}$$ $${\sigma }_a=\text{alternating stress (or stress amplitude)}=\left|\frac{{\sigma }_{\text{max}}-{\sigma }_{\text{min}}}{2}\right|$$ $${\sigma }_r=\text{stress range}$$ $$R=\text{stress ratio}=\frac{{\sigma }_{\text{min}}}{{\sigma }_{\text{max}}}$$

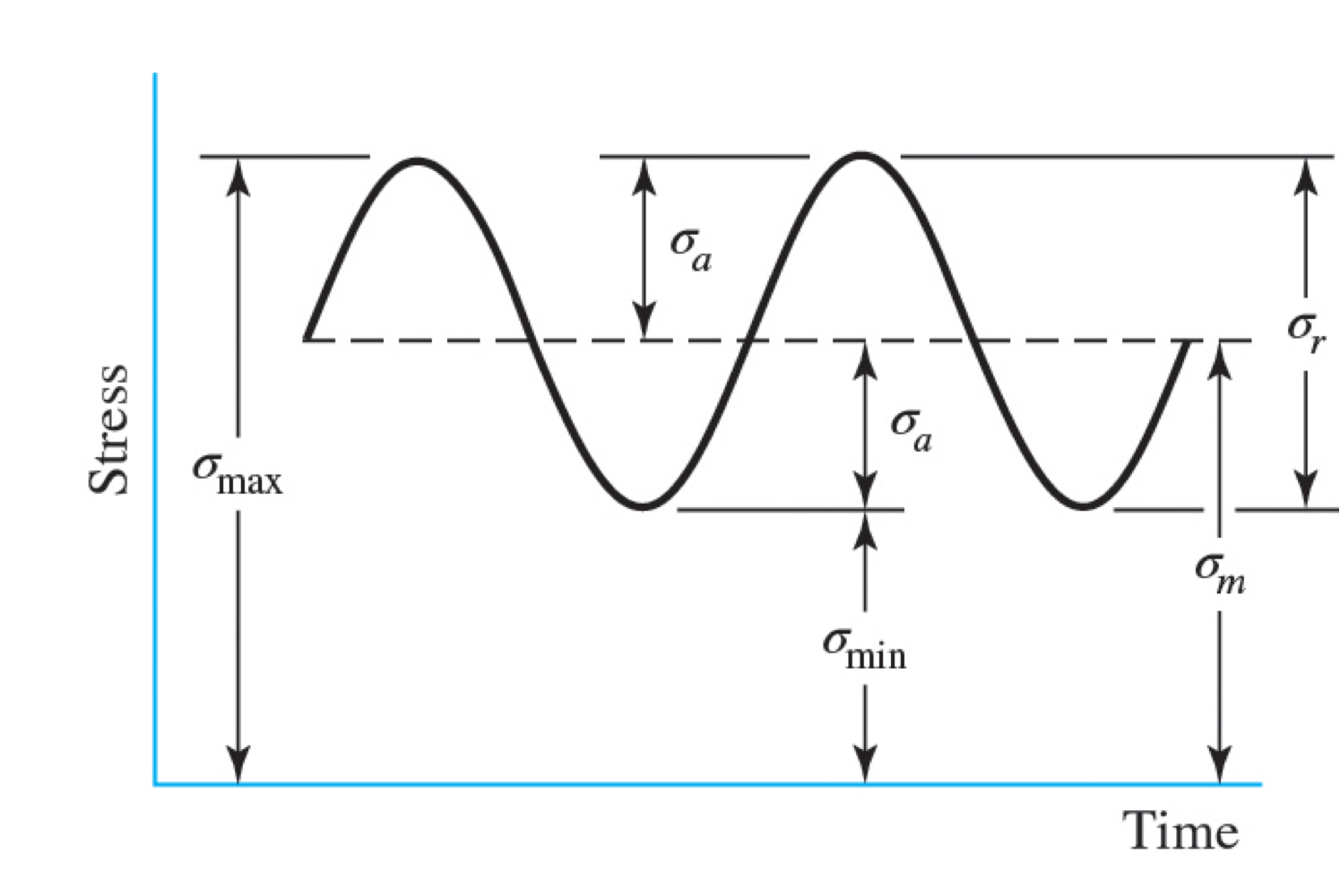
Repeated stress occurs when minimum stress is 0

Completely reversed stress occurs when mean stress is 0, in this case alternating stress is sigma_ar and these are the stress cycled between magnitudes of tensions and compression.

S-N Diagrams

Based on rotating-beam test under completely reversed stress cycling conditions

These graphs show the ultimate strength of a material vs its fatigue strength over different life cycles (low, high, infinite)

Basquin’s Equation describes the relationship between an applied stress and the number of cycles to failure:

$S_f=a{N}^b$

Finding Fatigue (f)

You can use Basquin’s or the S-N curve (y-axis) to find f (the fatigue strength point)
If $70<S_{ut}<200\text{ kpsi}$:
$f=1.06-2.8\left(10^{-3}\right)S_{ut}+6.9\left(10^{-6}\right)S_{ut}^2$
If $500<S_{ut}<1400\text{ MPa}$:
$f=1.06-4.1\left(10^{-4}\right)S_{ut}+1.5\left(10^{-7}\right)S_{ut}^2$

Low Cycle S-N Line

Use this analysis for fatigue failures between 1 and $10^3$ cycles Using Basquin’s Equation which also comes in this form
$\log \left(S_f\right)=b\log \left(N\right)+\log \left(a\right)$
Using given values you can find a and b and then use then to find $S_f$

$a=S_{ut}$ $b=-\frac{1}{3}\log f$

High-Cycle S-N Line

Use this analysis for fatigue failures between $10^3$ and $10^6$ cycles
$a=\frac{{\left(f{S}_{ut}\right)}^2}{S_e}$
$b=-\frac{1}{3}\log \left({\frac{fSut}{S_e}}_{}\right)$
Where these definitions can be used to solve for N
$N={\left({\frac{{\sigma }_{ar}}{a}}_{}\right)}^{\frac{1}{b}}$
Remembering that alternating stress $sigm{a}_{ar}$ is
${\sigma }_{ar}=\left|\frac{{\sigma }_{\max }-{\sigma }_{\min }}{2}\right|$
Which is the stress amplitude

Points of interest and Piecewise for SE!!!

In general, $S{e}^{\prime }$ is…

$$f(S_{ut})=\{\begin{array}{ll}100,& \text{if }{S}_{ut}>200\text{ Kpsi}\\ 700\text{ MPa},& \text{if }{S}_{ut}>1400\text{ MPa}\\ 0.5S_{ut},& \text{if }{S}_{ut}\le 200\text{ Kpsi}\text{ (1400 MPa)}\end{array}$$

So $S_e$ is dependant on the value of $S_{ut}$

Steels are good

For steels, Se ~= Se’!!! This was you don’t need to calculate all the k’s

Aluminium Alloy's are weird

No endurance limit
Use fatigue strength at N = 5x10^8 cycles
Can find in Table A-25

For cycles of magnitudes, the limit is:
$10^3\to f{S}_{ut}$
$10^6\to S_e$
Insert specific case into the following equation to two sets of equations, then use substitution to get a and b which are given above
$\log S_f=b\log N+\log a$

Solving Generally

• Find $S_e$ based off of test specimen ($S_{ut}$)
• Find f from S-N curve or use equation (if its off the graph use maximum value in one direction)
• Use a and b formulas to solve for a and b using $S_{ut}$ and $S_e$
• Use a and b to solve for $S_f$ or N