Three Phase Circuits

Note

Composed of three single phase A.C circuits

Three phase power systems provide greater power density than a single phase AC circuit with the same current.

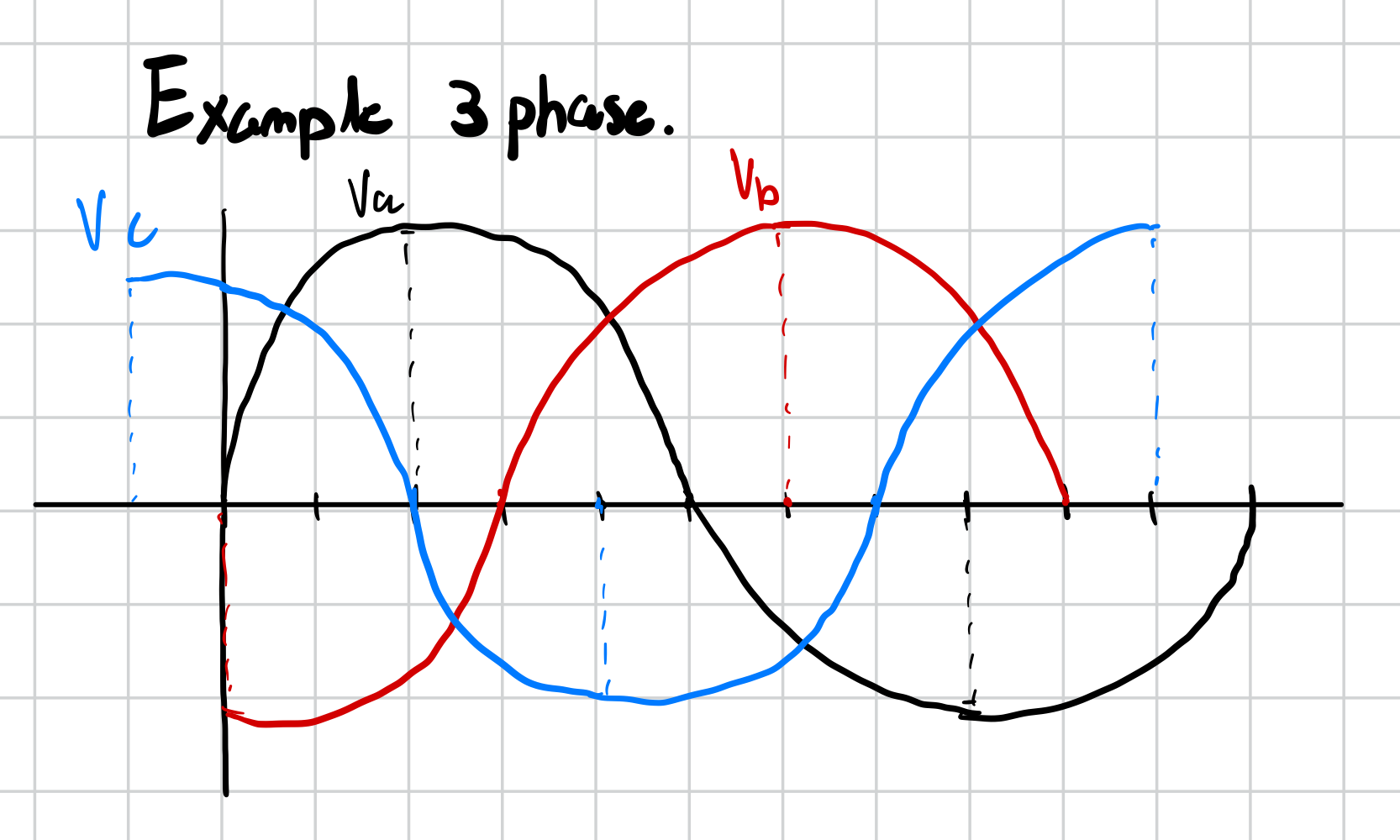
Each phase is shifted to the right by 120 degrees.
$v_a=\sqrt{2}V\cos \left(\omega t+{\theta }_v\right)$
$v_b=\sqrt{2}V\cos \left(\omega t+{\theta }_v-120\right)$
$v_c=\sqrt{2}V\cos \left(\omega t+{\theta }_v-240\right)=\sqrt{2}V\cos \left(\omega t+{\theta }_v+120\right)$ Written in Phasors:
$V_a=V<{\theta }_v$
$V_b=V<{\theta }_v-120$
$V_c=V<{\theta }_v+120$
If viewed on a cartesian plane, all three voltages are spaced out evenly by 120° (360° / 3 = 120°).

Tip

The algebraic sum of $V_a$, $V_b$, and $V_c$ is = 0 making it a balanced 3 phase source.

Loads

In terms of loads, if the impedances of each A.C circuit is equal, the loads are balanced. Otherwise, they are unbalanced.

Connections Styles

Y or Star Connection

One terminal of each phase is connected to the same terminal of the other phases making a neutral point.

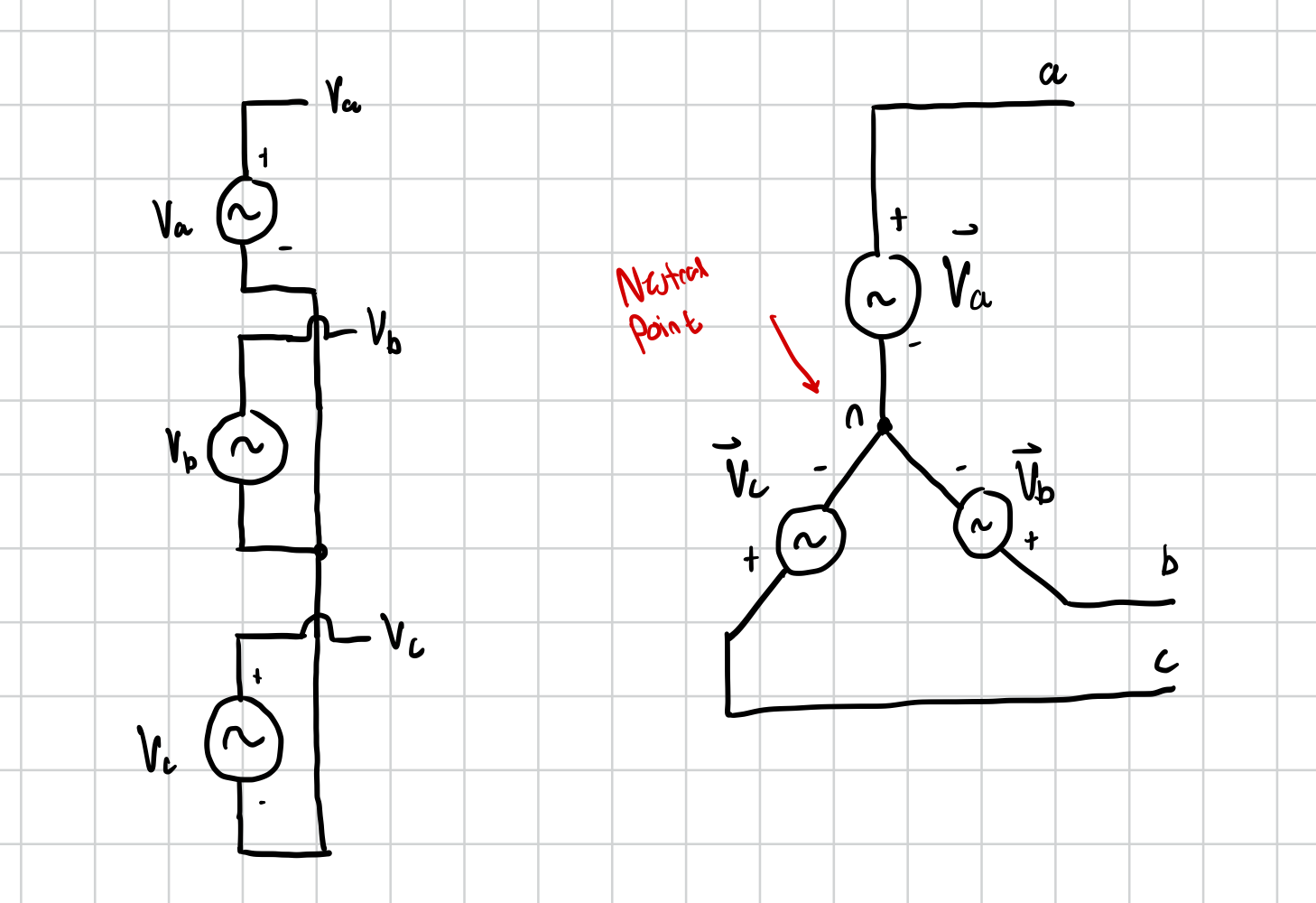
From the phase to neutral voltages, one can find the phasors of the line-to-line voltages (voltage differences between the phases themselves)

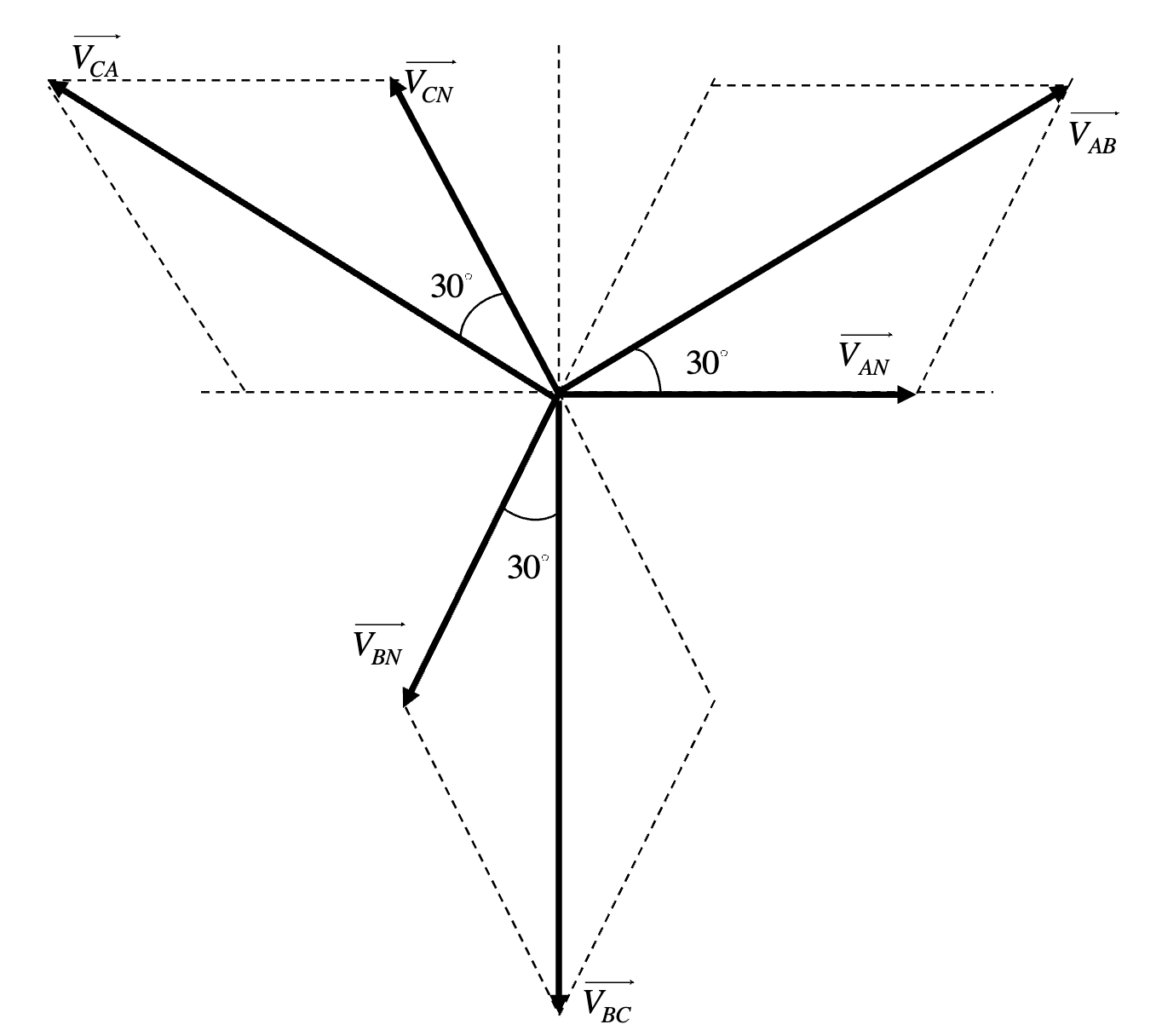
Through geometry, the phasors of the line to live voltages can be expressed as: $V_{AC}=V_{LL}<30°$
$V_{BC}=V_{LL}<-90°$
$V_{CA}=V_{LL}<150°$
where $V_{LL}=\sqrt{3}{V}_{phase}$
In general if we are given a 3 phase system (ex. 400 kV @ 60hz, this is line-to-line if not otherwise specified).

Currents

In terms of currents, if the loads are balanced, and the voltages are balanced (they are all the same) then… $\overrightarrow{I_a}=I_a<-\theta$
$\overrightarrow{I_b}=I_b<-\theta -120$ $\overrightarrow{I_c}=I_c<-\theta +120$
Also the sum of $I_a$ + $I_b$ + $I_c$ is = 0.

When computing currents, you use a line-to-neutral voltage (ex, $V_{an}$, or $V_{bn}$).

Tip

If the system is not balanced, if you connect the neutrals of the impedance and the sources to carry the current, you can model a three phase balanced system as three single phase systems and solve it with phasors three times as single phase systems. This is because the voltages, currents and angles are not guaranteed to be equal.

Tip

If the system IS balanced, then I_n is 0 and the red circled part is a single phase problem, where the neutrals are VIRTUALLY connected. You only need to solve one single phase problem here and then add or subtract the next corresponding phase shift from the obtained value to get the next value.

Tip

Y Connections allows feeding single phase loads!!!

Y Connection Relationships

Tip

Phi is always the angle between a phase to neutral voltage (V_an), and phase current (I_an).

Connection Sequence

Phasor sequence connection is very important in A.C machines in dictation the direction of torque.

Solving Basic Questions

1. Find the line current by using $I_{La}=I_a={\frac{V_{AN}}{Z+Z_{Line}}}_{}$
2. You can solve for the different types of power using the Power equations where phi can be found by using the given load impedance (Z)
3. You can solve for power factor using phi, remember that the PF for the load and source will be different depending on if there is a line impedance, if there isn’t they will be the same

Delta Connections

See Delta Connections