Failure Theories

Ductiles

${ϵ}_f\ge 0.05$
To determine yield criteria

• Maximum shear stress
• Distortion energy
• Ductile Coulomb-Mohr

Brittles

${ϵ}_f<0.05$
To determine fracture criteria

• Maximum shear stress
• Distortion energy
• Ductile Coulomb-Mohr

Failure Theory

It is important to place an upper limit on the state of stress that defines material properties

No single theory of failure can be applied to specific materials at all times since materials act differently depending on numerous factors

• Temperature
• Rate of loading
• Geometry

Goal of problems

Need to calculate normal and shear stress at points where they are the largest in the member

Therefore
We need to establish the state of stress → then the principle stresses at these critical points (using Mohr’s Circle or Stress and Stress Transformation)

Nominal stress to sigma x and y

Nominal stresses are Sigma X when they cause bending, and Sigma Y when they cause shearing

Ductile Materials

Maximum Shear Stress Theory

Slipping:

• Most common type of yielding of ductiles (materials like steel)
• Occurs along the contact planes of randomly ordered crystals that makeup a material (along the Luder Lines)
• Slipping occurs due to shear stress
• Can be found using Mohr’s Circle
  • Then ${\tau }_{\max }=\frac{{\sigma }_y}{2}$
  • This stress acts on the plane that is 45° from the planes of principle stress (remembering that on a Mohr’s circle angles are doubled)
• Using this idea, Tresca proposed the maximum shear stress (or Tresca) theory
  • Yielding of materials begins when absolute maximum shear stress in the material reaches the shear stress than causes the same material to yield when it subject only to axial tension
  • To avoid failure, tau_max in materials must be less than or equal to sigma_y/2

Slipping Condition

${\tau }_{\max }\le \frac{{\sigma }_y}{2}=\frac{{\sigma }_1}{2}$

3D

Note that you may need to consider 3D stresses in 3 principle directions
Here, sigma_1 is the maximum stress and sigma_3 is the minimum stress

There are also three principle shears now where the notation tau_1/3 dictates the difference between sigma_1 - sigma_3

In the General Case

${\tau }_{\max }={\frac{{\sigma }_1-\sigma 3}{2}}_{}\ge {\frac{Sy}{2}}_{}$
Yield Strength:
$S_{sy}=0.5S_y$
When designing with a factor of safety n:
${\tau }_{\max }={\frac{{\sigma }_1-\sigma 3}{2}}_{}=\frac{S_y}{2n}$
For two principal stresses in the plane of analysis (where sigma_A > sigma_B) and the third principle stress is 0…

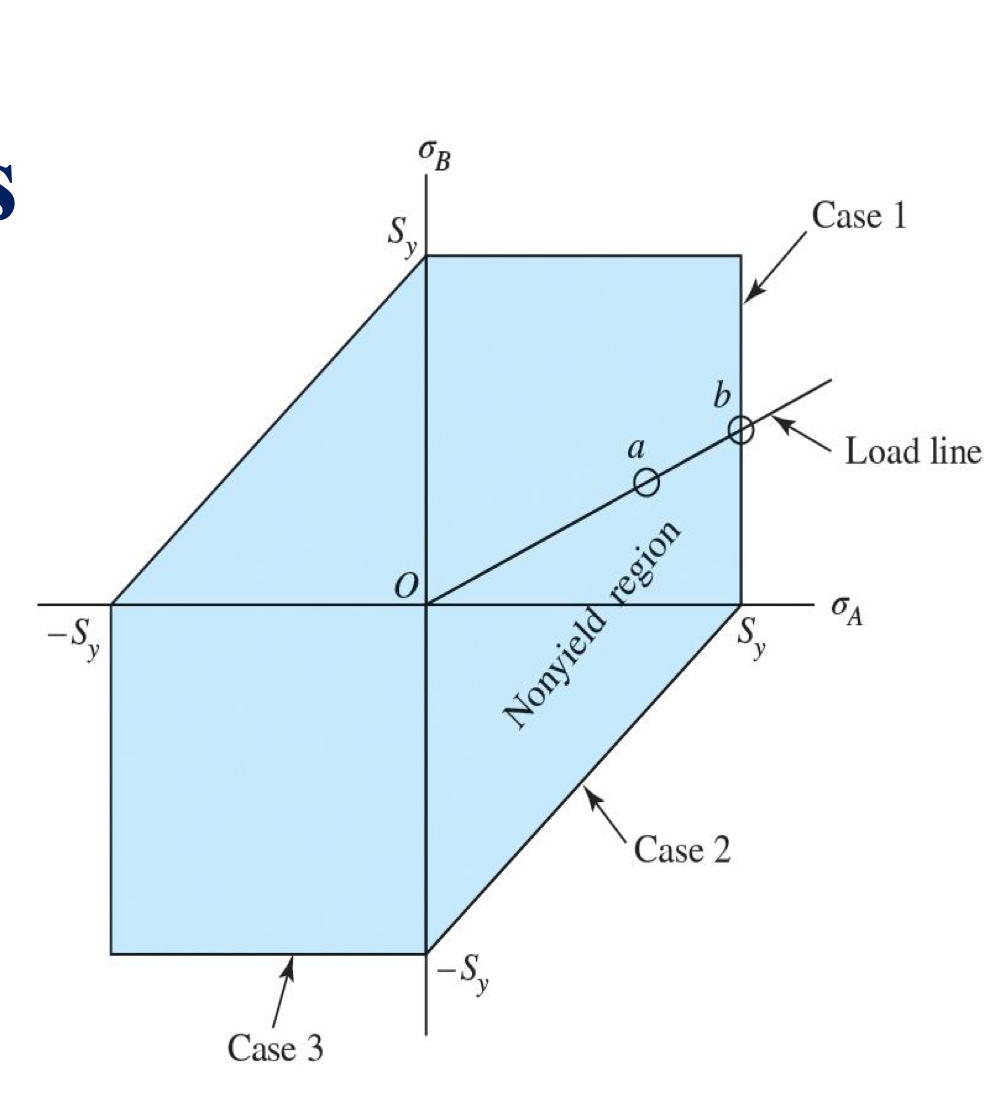
Solving

Basically the idea here is that for 3D cases, we calculate the principle stresses (sigma_A and sigma_B where sigma_A is greater than sigma_B) and use the Stress and Stress Transformation principle stress equations with the following cases to get the yield criteria based on the specific case of sigma_A and sigma_B that we get.

$\text{Case 1:}{\sigma }_A\ge {\sigma }_B\ge 0$
${\sigma }_1\ge {\sigma }_A\text{and}{\sigma }_3=0$ $\text{Yield:}{\sigma }_A\ge S_y$
$\text{Design: }{\sigma }_A=\frac{S_y}{n}$
$\text{Case 2:}{\sigma }_A\ge 0\ge {\sigma }_B$
${\sigma }_1={\sigma }_A\text{and}{\sigma }_3={\sigma }_B$ $\text{Yield:}{\sigma }_A-{\sigma }_B\ge S_y$ $\text{Design:}{\sigma }_A-{\sigma }_B=\frac{S_y}{n}$
$\text{Case 3:}0\ge {\sigma }_A\ge {\sigma }_B$ ${\sigma }_1=0\text{and}{\sigma }_3={\sigma }_B$
$\text{Yield:}{\sigma }_B\le -S_y$ $\text{Design:}{\sigma }_B=-\frac{S_y}{n}$

Distortion Energy Theory

*For Ductile Materials
Yielding occurs when the distortion strain energy per unit volume reaches distortion strain energy per unit volume for simple compression or tension of the same material

Ordering

Once again also assuming that sigma_1 is the largest stress and sigma_3 is the minimum stress

${\sigma }_{avg}=\frac{{\sigma }_1+{\sigma }_2+{\sigma }_3}{3}$

Derivation of the Von Mises Stress Equation

Where u is the strain energy per unit volume
$u=\frac{1}{2}ϵ\sigma$
$u=\frac{1}{2E}\left({\sigma }_1^2+{\sigma }_2^2+{\sigma }_3^2-2\nu \right)$

For the General Case

${\sigma }^{\prime }={[\frac{{\left({\sigma }_1-{\sigma }_2\right)}^2+{\left({\sigma }_2-{\sigma }_3\right)}^2+{\left({\sigma }_3-{\sigma }_1\right)}^2}{2}]}^{\frac{1}{2}}\ge S_y$ When you’re designing with a factor of safety
${\sigma }^{\prime }=\frac{S_y}{n}$
Note that $S_{sy}={\frac{S_y}{\sqrt{3}}}_{}$

For Plane Stress

In normal stress, the von Mises Stress and yield conditions can be found as follows
${\sigma }^{\prime }={\left({\sigma }_A-{\sigma }_A{\sigma }_B+{\sigma }_B^2\right)}^{\frac{1}{2}}\ge S_y$
For Design:
${\sigma }^{\prime }=\frac{S_y}{n}$

Yield conditions:

${\left(3{\tau }_{xy}^2\right)}^{\frac{1}{2}}={\sigma }^{\prime }\ge S_y$
${\tau }_{xy}\ge \frac{{\tau }_{xy}}{\sqrt{3}}$
For Design:
${\sigma }^{\prime }={\tau }_{xy}\sqrt{3}=\frac{S_y}{n}$
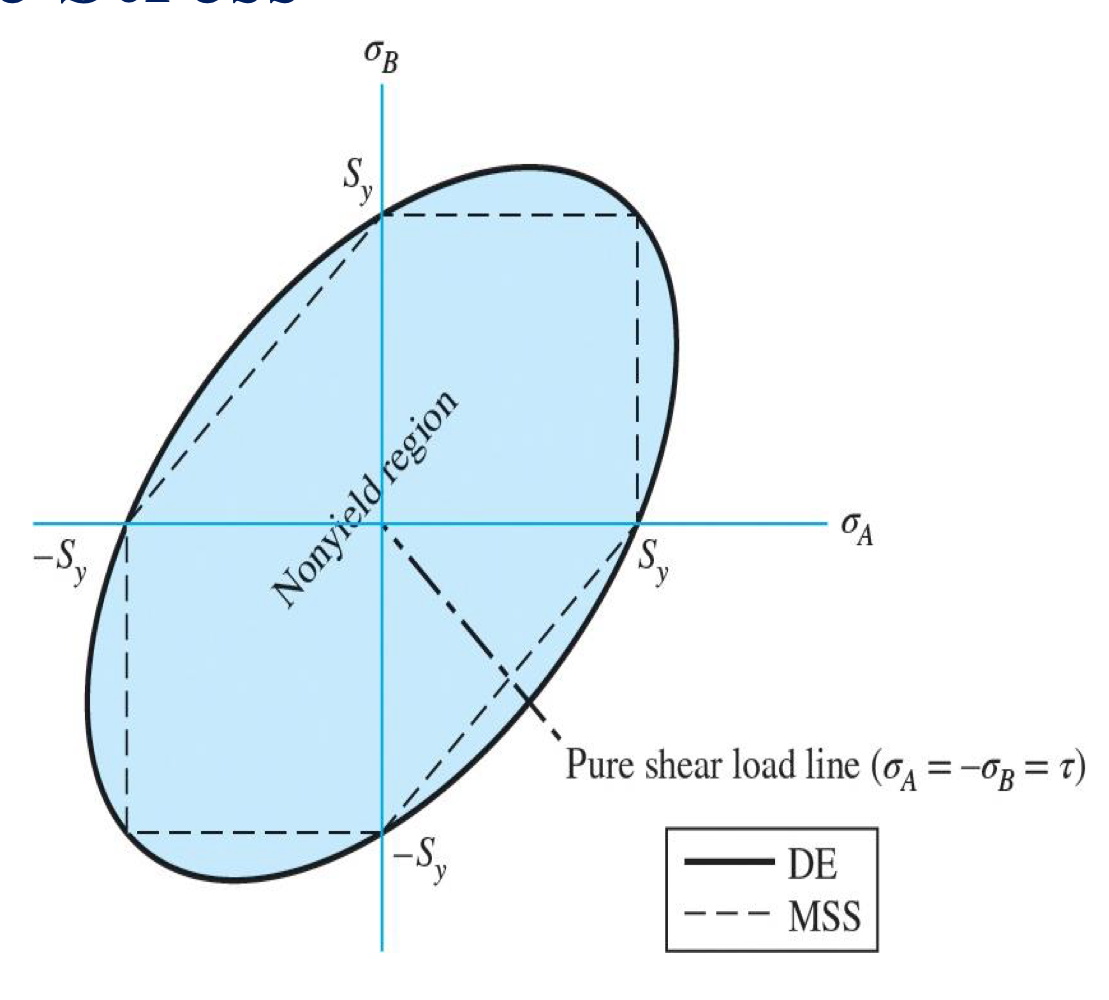
Comparing to MSS theory, DE theory has a higher shear yield strength than MSS theory.

Also note that in this case
${\sigma }_A=-{\sigma }_B$

Equations in terms of xyz

The equations for DE theory in terms of xyz are as follows:
General Case:
${\sigma }^{\prime }=\frac{1}{\sqrt{2}}{\left[{\left({\sigma }_x-{\sigma }_y\right)}^2+{\left({\sigma }_y-{\sigma }_z\right)}^2+6({\sigma }_z-{\sigma }_x+6\left({\tau }_{xy}^2+{\tau }_{yz}^2+{\tau }_{zx}^2\right)\right]}^{\frac{1}{2}}$
Plane Stress:
${\sigma }^{\prime }={\left({\sigma }_x^2-{\sigma }_x{\sigma }_y+{\sigma }_y+3{\tau }_{xy}^2\right)}^{\frac{1}{2}}$
Where the yield and design conditions remain unchanged.

Coulomb-Mohr Theory

For ductile materials
Used for materials where strength is tension does not equal strength in compression

The idea here is we want to find the Mohrs failure curve which is tangent to the three failure circles

You can use the results of tensile, compressive and shear stress to construct the three failure circles to define a failure envelope

In this theory, we assume the tangent line is straight for the three circles and failure only depends on tensile and compressive strengths

The General Case

The Yield Condition in this case
$\frac{{\sigma }_1}{S_t}-{\frac{{\sigma }_3}{S_C}}_{}\ge 1$
When designing:
${\frac{\sigma 1}{S_t}}_{}-\frac{{\sigma }_3}{S_C}=\frac{1}{n}$
For Plane Stress
Similar to MSS, there are two principal stresses calculated using Stress and Stress Transformation in the plane of analysis where sigma_A > sigma_B and the third principal stress is 0

The cases:
$\text{Case 1:}{\sigma }_A\ge {\sigma }_B\ge 0$ ${\sigma }_1={\sigma }_A\text{and}{\sigma }_3=0$ $\text{Yield:}{\sigma }_A\ge S_t$
$\text{Design:}{\sigma }_A=\frac{S_t}{n}$ $\text{Case 2:}{\sigma }_A\ge 0\ge {\sigma }_B$

${\sigma }_1={\sigma }_A\text{and}{\sigma }_3={\sigma }_B$ $\text{Yield:}\frac{{\sigma }_A}{S_t}-\frac{{\sigma }_B}{S_c}\ge 1$ $\text{Design:}\frac{{\sigma }_A}{S_t}-\frac{{\sigma }_B}{S_c}=\frac{1}{n}$
$\text{Case 3:}0\ge {\sigma }_A\ge {\sigma }_B$

${\sigma }_1=0\text{and}{\sigma }_3={\sigma }_B$ $\text{Yield:}{\sigma }_B\le -S_c$
$\text{Design:}{\sigma }_B=-\frac{S_c}{n}$

Shear Stress

For pure shear:
${\sigma }_x={\sigma }_y=0$
and
${\sigma }_1=-{\sigma }_3=\tau$
The yield conditions in this case
${\tau }_{\max }=\frac{S_{sy}}{n}$
and
${\sigma }_1=-{\sigma }_3=\frac{S_{sy}}{n}$
The relationship between shear strength, tension yield strength and compression yield strength are as follows
$S_{sy}={\frac{S_{yt}{S}_{yc}}{S_{yt}+S_{yc}}}_{}$

When to use each case?

MSS

• Quick and easy and conservative
• Useful for design DET
• Need to carefully consider the n value
• Use when you want to learn why a specific part failed CMT
• Use when yield strengths are unequal in tension and compression
• Use for megnaesium allows and grey cast irons?