Mohr's Circle

Mohr's Circle

Preventing failure, a design needs to account for maximum stress resulting from normal and shear stresses

The Mohr’s Circle:

• Studies the combined state of all stresses
• Helps identify max stresses
• Is a visual representation

Using the equation of a circle:
$x^2+y^2=R^2$ where $x^2$:
$\sigma -\frac{{\sigma }_x-{\sigma }_y}{2}$
$y^2$:
${\tau }^2$
$R^2$:
$\frac{{\left({\sigma }_x-{\sigma }_y\right)}^2}{2}+{\tau }_{xy}^2$
Diagram

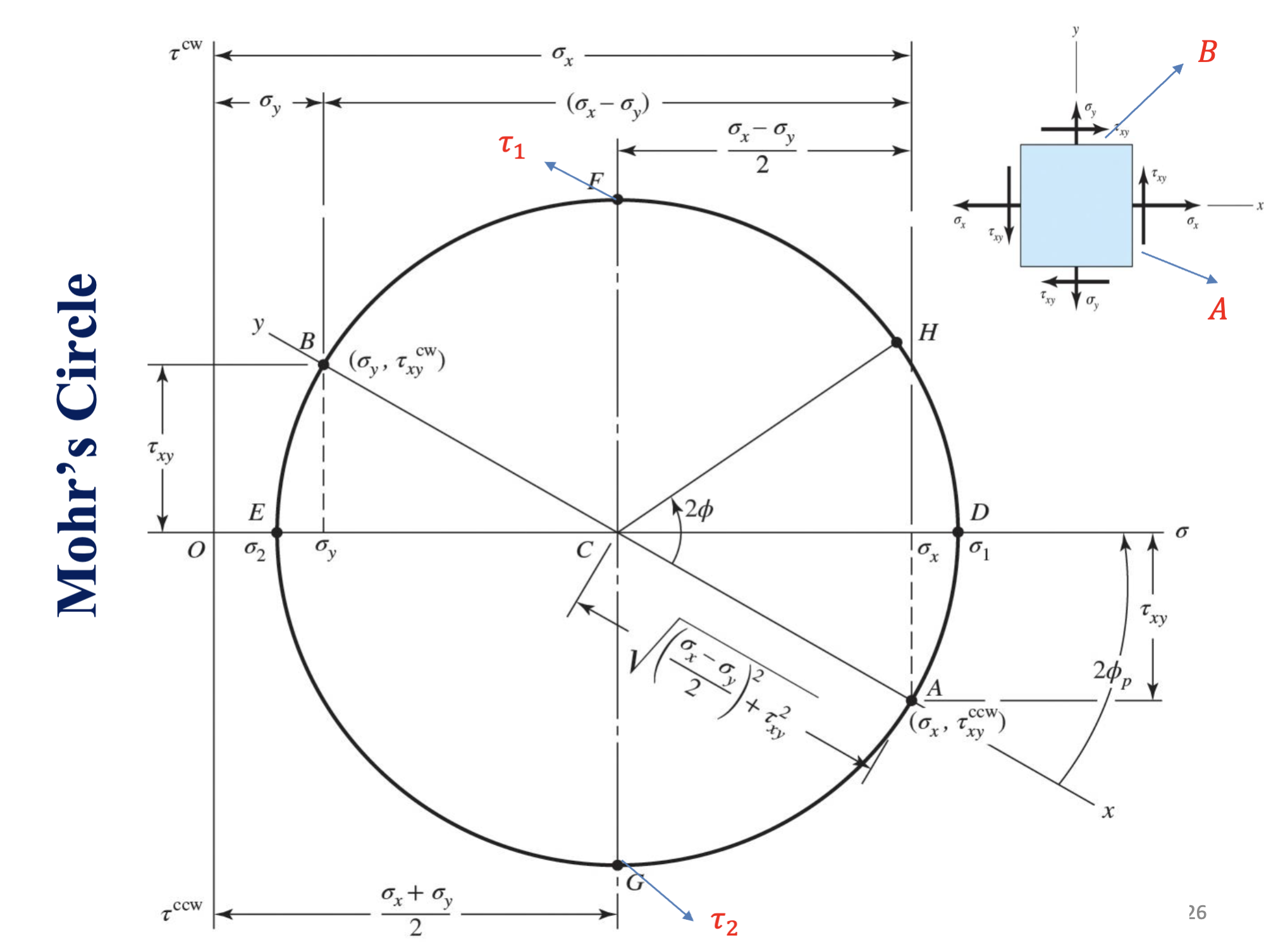
Where E in minimum stress, and D is maximum stress.
The top face of a Stress and Stress Transformation diagram is point B, and the right-most face is point A.

Conventionally:

• Shear stresses that rotate an element clockwise are above the sigma axis
• Shear stresses that rotate an element counter-clockwise are below the sigma axis

Drawing a Mohr’s Circle

1. Locate the center C = $\left(\frac{{\sigma }_x+{\sigma }_y}{2},0\right)$
2. Find CD $C=\left(\frac{{\sigma }_x-{\sigma }_y}{2},0\right)$
3. Locate the face of A $\left({\sigma }_x,{\tau }_{xy}\right)$
4. Locate the face of B $\left({\sigma }_y,{\tau }_{xy}\right)$
5. Connect A B and C and draw a circle
6. Use geometry to compute the rest (principle stresses, max shear stress = R, principle angles, etc)

Mohrs Circle Angles

Angles in a Mohr’s circle are doubled (the angle between C, A, and the sigma axis):
$\tan \left(2{\varphi }_p\right)=\frac{A_y}{CD-OC}$

Orientation

Max shear and average normal stress are always 45 degrees rotated CCW from max normal stress (${\varphi }_p$)

More on orientation

The sign of ${\varphi }_p$ is determined by the sign of tau_xy (+ = cw)

If one is cw the other is ccw!

When determining angle we are either subtracing 45 degrees from ${\varphi }_p$, or ${\varphi }_p$ form 45 degrees. If ${\varphi }_p$ > 45 degrees: ${\varphi }_s={\varphi }_p-45$
otherwise: ${\varphi }_s=45-{\varphi }_p$

In 3D

Now there are three principle directions and stresses

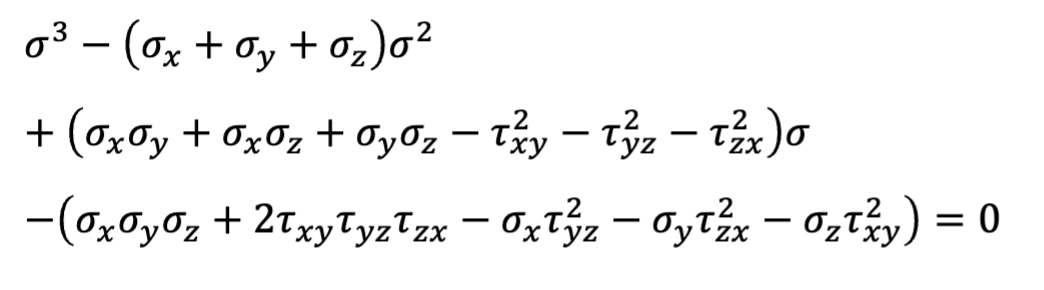
There are also 3 principle shears now