Frequency Domain Analysis

Frequency

In systems, this is a man made concept whereas the time domain is a physical concept.

The output of a linear Dynamic Systems is the transient response + the steady state response $x\left(t\right)=H\left(s\right)e^{st}$

We can represent a time signal as a sum of sinusoids and for any single sinusoid, we can represent that as a combination of sinusoids

If $s=j\omega$ (on the imaginary axis), then $H\left(j\omega \right)$ is the system’s frequency response.

Where $e^{st}$ can be represented using Euler’s Identity

Frequency response is the steady-state response to a sinusoid (after the transient response disappears)

$x\left(t\right)=\left|H(j\omega t\right|e^{j\omega t+<H\left(j\omega \right)}$
Where the first term is the amplification by the system and the second term is the phase shift by the system.

If we say that $f\left(t\right)=A\sin {\omega }_t$ then the output $x\left(t_{}\right)=A\left|H\left(j{\omega }_{}\right)\right|\sin \left(\omega t+\varphi \right)$ where $\varphi =<J\left(j\omega \right)$

Applications to 1st Order Systems

$m{v}^{\prime }\left(t\right)+cv\left(t\right)=f\left(t\right)$
$f\left(t\right)=A\sin \omega t$
Transforming to the frequency domain…
$H\left(s\right)=\frac{V\left(s\right)}{F\left(s\right)}=\frac{1}{ms+c}$
so $\tau =\frac{m}{c}$
If we say that $s=j\omega$ then $H\left(j\omega \right)=\frac{1}{mj\omega +s}=\frac{1}{c\sqrt{{\tau }^2{\omega }^2+1}}$
Where the angle $<H\left(j\omega \right)=-{\tan }^{-1}\left(\frac{m\omega }{c}\right)={\tan }^{-}1(\omega \tau )$
Examining this at steady state…
$v{\left(t\right)}_{steady}=A\frac{1}{c\sqrt{{\tau }^2{\omega }^2+1}}\sin \left[\omega t+\left(-{\tan }^{-1}\left(\omega \tau \right)\right)\right]$

Applications to Second Order Systems

Of this form…
$m{x}^{{}^{\prime \prime }}+c{x}^{\prime }+kx=f\left(t\right)$ Taking to the LaPlace domain…
$H\left(s\right)=\frac{X\left(s\right)}{F\left(s\right)}=\frac{1}{m{s}^2+cs+k}$
The over-damped case $\zeta >1$
Two real poles of $s_1$ and $s_2$
$H\left(s\right)=\frac{\frac{1}{k}}{\frac{m}{s}{s}^2+\frac{c}{k}s+1}=\frac{\frac{1}{k}}{\left(s-s_1\right)\left(s-s_2\right)}$
Once again subbing in $s=j\omega$
$H\left(j\omega \right)=\frac{\frac{1}{k}}{\left(j\omega -s_1\right)\left(j\omega -s_2\right)}$
The underdamped case $0<\zeta <1$
$H\left(s\right)=\frac{1}{m{s}^2+cs+k}=\frac{\frac{1}{m}}{s^2+\frac{c}{s}s+\frac{k}{m}}$
Resulting in $H\left(s\right)=\frac{\frac{1}{m}}{s^2+2\zeta {\omega }_{n}s+{\omega }_{n^2}}$ where…
${\omega }_n=\sqrt{\frac{k}{m}}$
$\zeta =\frac{c}{2\sqrt{\mathrm{km}}}$
Dividing by ${\omega }_m^2$ you send up with the frequency ratio as a term in the denominator $r=\frac{\omega }{{\omega }_n}$
Simplifying, we end up with…
$\left|H\left(j\omega \right)\right|=\frac{\frac{1}{k}}{\sqrt{{\left(1-r^2\right)}^2+{\left(2\zeta r\right)}^2}}$
$<H\left(j\omega \right)=<\frac{1}{k}-<\left(1-r^2+j2\zeta r\right)=-\tan \frac{2\zeta r}{1-r^2}$
Summary Table

	|H|	<H
$\omega =0$ and $r=\frac{\omega }{{\omega }_n}=0$	$\frac{1}{k}$	0
${\omega }_{}={\omega }_n$ and $r=1$	$\frac{1}{2\zeta k}$	$-\frac{\pi }{2}$
r→$\infty$	0	$-\pi$

Notes from solving

To solve the steady-state response of a function, you need to:

• Find a 1st order ODE
• Do the LaPlace transform
• Find the transfer function
• Find the magnitude of the transfer function
• Find the phase angle of the transfer function
• Assemble the steady-state response function in the following form $y_{ss}\left(t\right)=A\left|H\left(s\right)\right|\sin \left(\omega t<H\left(s\right)\right)$

For a second order system
Expand to the form $s^2+as+b$ and convert to ${\left(j\omega \right)}^2+aj\omega +b$ which yields $\left(-{\omega }^2+b\right)+\left(a\omega j\right)$ which are your real and imaginary parts, then its just like normal.

If your system has multiple parts like $T\left(t\right)=20+15\sin 3t+6\cos \left(5t\right)$ then solve with the $\omega$s from each section (in this case its $\omega =0$ $\omega =3$ and $\omega =5$) and then follow the steady-state response function form to piece it all back together (there will be three terms where the all real term is something like $20\left|H\left(0\right)\right|$)

---

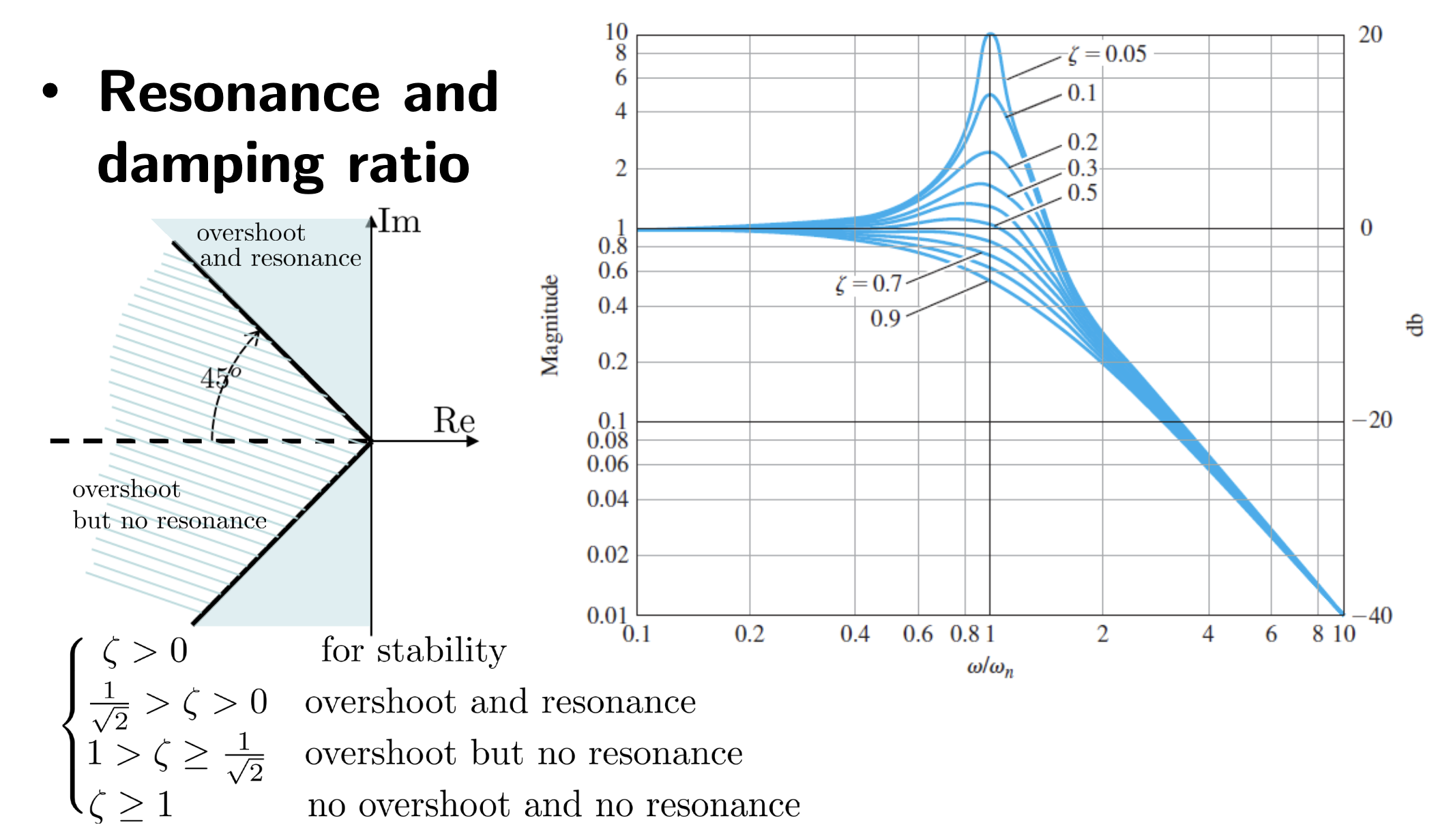
Frequency Domain Specifications

1. Resonance peak $M_r$: maximum value of $M_G:=\Vert G\left(j\omega \right)\Vert$ this is not desirable and we should suppress this.
2. Resonance frequency ${\omega }_r$ which is the frequency required to achieve $M_r$ 1.
3. Bandwidth, ${\omega }_{BW}$: range of frequency that a system can normally operate, this is where the $M_G$ drops to $\frac{1}{\sqrt{2}}$ of the DC gain
4. Cutoff rate: the rate at which the high frequency signals are attenuated and is the slope of $M_G$ (in dB) at high frequencies which depend on relative the relative degree of the system (n - m (denominator degree - numerator degree))

For 1st order systems
For a standard form of $G\left(s\right)=\frac{K}{\tau s+1}=\frac{K}{tj\omega +1}=\frac{K\left(1-\tau \omega j\right)}{1+{\tau }^2{\omega }^2}$

1. Resonance Peak
   • For a first order system: $M_G={\left|G\left(j\omega \right)\right|}_{dB}=20{\log }_{10}\left|\frac{K}{\tau j\omega +1}\right|=20{\log }_{10}K-20{\log }_{10}\sqrt{{\tau }^2{\omega }^2+1}$
   • Where $M_G$ is a decreasing function of $\omega$, thus there is n peak or resonance
2. Resonance Frequency
   • No resonance for a 1st order system
3. Bandwidth
   • For a first order system $M_G=\frac{K}{\sqrt{1+{\tau }^2{\omega }^2}}=\frac{1}{\sqrt{2}}K\Rightarrow {\omega }_{BW}=\frac{1}{\tau }$
4. Cutoff Rate
   • -20 dB/decade

For 2nd order systems
For a standard form of $G\left(s\right)=K\frac{{\omega }_n^2}{s^2+2\zeta {\omega }_n+{\omega }_n^2}$ which can be represented as…
$G\left(j\omega \right)=K\frac{{\omega }_n^2}{-{\omega }^2+2\zeta {\omega }_{n}j\omega +{\omega }_n^2}=K\frac{1}{\left(1-{\left(\frac{\omega }{{\omega }_n}\right)}^2\right)+j\left(2\zeta \frac{\omega }{{\omega }_n}\right)}=K\frac{1}{\left(1-u^2)+j\left(2\zeta u\right)\right)}$ where $u=\frac{\omega }{{\omega }_n}$

1. Resonant Peak and Resonance Frequency
   • $M_G\left(\omega \right)=K\frac{1}{\sqrt{{\left(1-u^2\right)}^2+{\left(2\zeta u\right)}^2}}=K\frac{1}{f\left(u\right)}$
   • Where ${\left(f\left(u\right)\right)}^2={\left(1-u^2\right)}^2+{\left(2\zeta u\right)}^2=u^4-2\left(1-2{\zeta }^2\right)u^2+1$
   • Completing the square… this is the same as ¯${\left(u^2-\left(1-2{\zeta }^2\right)\right)}^2+4{\zeta }^2\left(1-{\zeta }^2\right)$
   • If $1-2{\zeta }^2>0$ $f{\left(u\right)}^2$ has a minimum $4{\zeta }^2\left(1-{\zeta }^2\right)$ at $u^2=1-2{\zeta }^2$
   • If $\zeta <\frac{1}{\sqrt{2}},{\omega }_r={\omega }_n\sqrt{1-2{\zeta }^2}$ Where $M_G$ is a maximum here
     • The corresponding resonance peak is $M_r=\frac{K}{2\zeta \sqrt{1-{\zeta }^2}}$ where K is your open loop gain, this becomes $M_r=\frac{1}{2\zeta \sqrt{1-{\zeta }^2}}$ for the closed loop unity gain of 1
   • If $1-2{\zeta }^2\le 0$ then $f{\left(u\right)}^2$ is a minimum at $u=0$ and $\omega =0$
   • No resonance if $\zeta \ge \frac{1}{\sqrt{2}}$
   • We want this to be small
2. Bandwidth
   • ${\omega }_{BW}={\omega }_n{\left[\left(1-2{\zeta }^2\right)+\sqrt{4{\zeta }^4-4{\zeta }^2+2}\right]}^{\frac{1}{2}}$
   • $\zeta =\frac{1}{\sqrt{2}}$ gives the maximum bandwidth without resonance
   • We want this to be large
3. Cutoff Rate
   • 40 dB/decade