Worm Gears

Some Properties

• Non-intersecting orthogonal axes
• Can design them to prevent “backdriving”
• Poor efficiency (40-85%) friction
• High ratios obtainable in single stage
• High torque capacity
• Axial, radial, tangential forces

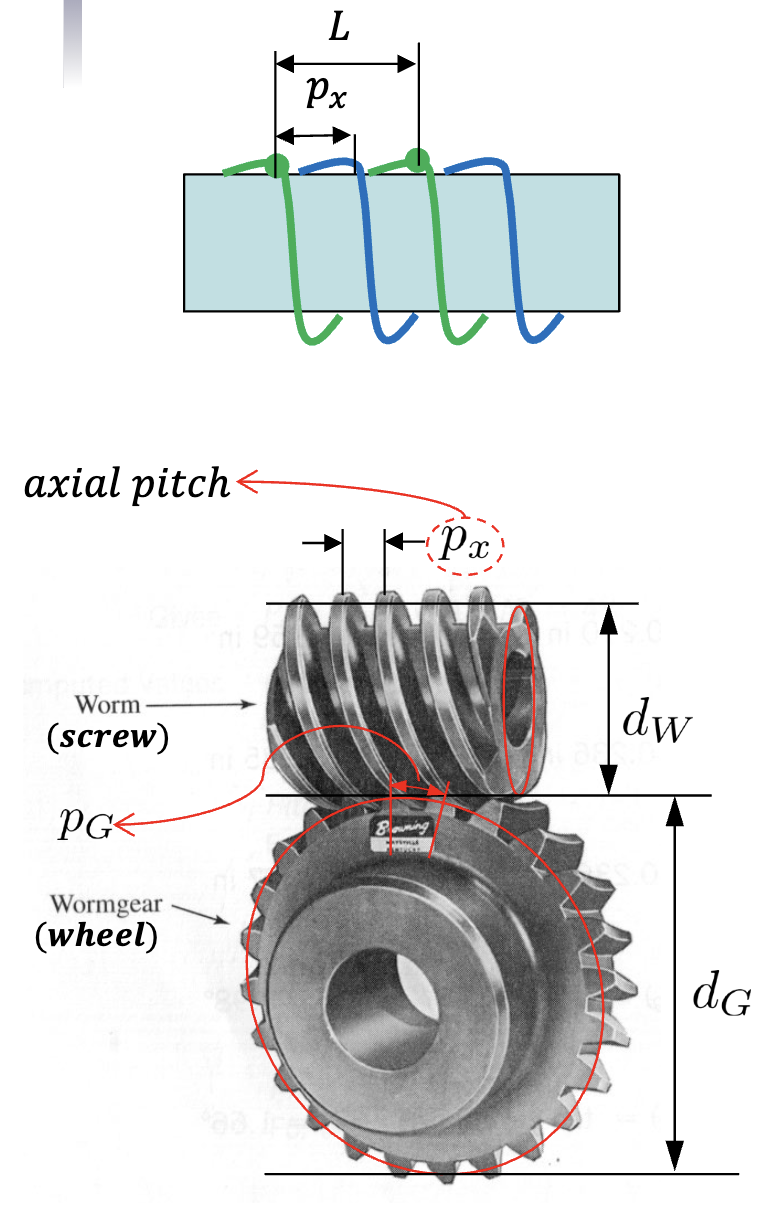
Worm Gear Diagram

We mate a worm (screw) with a gear

Some Nomenclature

• $d_w$ is the pitch diameter of the worm/screw
• $d_g$ is the pitch diameter of the wheel/gear
• $p_x$ is the axial pitch of the worm/screw
• $p_g$ is the circular pitch of the wheel/gear

Worms screws have a worm tooth number $N_w$ which is some start number which is used with $p_x$ to find the linear distance per revolution (360°) $L=N_w{p}_x$.

$p_x=p_g$ as well so for 1 rev of the worm screw, we move by $L$ on the worm screw and $N_w{p}_g$ on the wheel/gear.

Looking at the side on view of a worm screw…

Some notes from this side on view

• We typically care about the lead angle ($\lambda$) over the helix angle here, where $\lambda =90-{\psi }_w$
• A’’ is given as the vertical distance of one helical rotation along the lead angle

An important relationship here is…

• This is a rare case where $\frac{N_g}{N_w}\ne {\frac{d_g}{d_w}}_{}$
  • Instead, $L=N_w{p}_x=N_w{p}_g$
  • Or… $\frac{L}{\pi D_g}={\frac{N_w}{N_G}}_{}$
• $p_x=p_g=\frac{\pi d_g}{N_g}$
• The diameter of the worm screw is given by the following relationship
  • $\frac{C^{0.875}}{3.0}\le d_w\le \frac{C^{0.875}}{1.7},\left(C=\frac{d_w+d_g}{2}\right)$
• The relationship between face width and the diameter of the worm is…
  • $F_{\max }=0.67d_w$

Handedness

Worm gears also have handedness and the handedness is identified in the same way as with Helical Gears.
In this case, a RH worm is mated with a RH worm wheel (which contrasts to helical gears)
To determine axial load, turn your fingers in the direction of rotation and your thumb points in the direction of the axial load.

For the tangential load, you can also see in which direction the screw advancement occurs (left or right) which indicates the direction the worm wheel rotates which indicates the direction of the tangential force.

Driving

Only the worm screw can drive here, if the wheel tries to drive, the worm screw should lock.

Equations for Force

• $W_{xw}=W_n\cos {\varphi }_n\cos \lambda -\mu W_n\sin \lambda =W_n\left(\cos {\varphi }_n\cos \lambda -\mu \sin \lambda \right)$
• $W_{rw}=W_n\sin {\varphi }_n$
• $W_{tw}=W_n\cos {\varphi }_n\sin \lambda +\mu W_n\cos \lambda =W_n\left(\cos {\varphi }_n\sin \lambda +\mu \cos \lambda \right)$
• We also have a friction component $\mu W_n$ which is included in our equations above
• From these equations we can eliminate $W_n$…
  • $W_{rw}=W_{tw}\frac{\sin {\varphi }_n}{\cos {\varphi }_n\sin \lambda +\mu \cos \lambda }$
  • $W_{xw}=W_{tw}\frac{\cos {\varphi }_n\cos \lambda -\mu \sin \lambda }{\cos {\varphi }_n\sin \lambda +\mu \cos \lambda }$
• From the gears perspective…
  • Noting that radial loads at the same, and the axial loads and tangential loads in the other domain
  • $W_{xG}=W_{tG}\frac{\cos {\varphi }_n\sin \lambda +\mu \cos \lambda }{\cos {\varphi }_n\cos \lambda -\mu \sin \lambda }$
  • $W_{rG}=W_{tG}\frac{\sin {\varphi }_n}{\cos {\varphi }_n\cos \lambda -\mu \sin \lambda }$

Solving for Forces

When we model the worm, the Wr and Wx forces act in opposition, worms also have a moment created about a central axis caused by its axial force…

Here, we essentially, FBD the worm, write out our force balance equations and solve for our bearing loads in our planes of interest (usually 2 planes).

Then we solve for the axial and raidal forces on our bearings and Toque which is $T=\frac{d_w}{2}{W}_{xw}$

Efficiency

From the above axial, radial, and tangential equations, there are friction terms and no friction terms. Therefore, comparing our input to our output…
$\frac{W_{tw}}{W_{tG}}=\frac{W_n}{W_n}{\frac{\left(\cos {\varphi }_n\sin \lambda +\mu \cos \lambda )\right)}{\cos {\varphi }_n\cos \lambda -\mu \sin \lambda }}_{}\left(\frac{\frac{1}{\cos \lambda }}{\frac{1}{\cos \lambda }}\right)=\frac{\cos {\varphi }_n\tan \lambda +\mu }{\cos {\varphi }_n-\mu \tan \lambda }$

When assuming no friction…
$\frac{W_{tw}}{W_{tg}}={\frac{W_n\cos {\varphi }_n\sin \lambda }{W_n\cos {\varphi }_n\cos \lambda }}_{}=\tan \lambda$

From this derivation we can get efficiency…
$\eta =\frac{\cos {\varphi }_n-\mu \tan \lambda }{\cos {\varphi }_n+\mu \cot \lambda }$

Solving Worm Gear Tips

• Worms have a moment caused by the axial load when making an FBD of the worm from an axial perspective
• Output power is just efficiency multiplied by input power

The Right Hand Rule for Gears

• Wrap your fingers in the direction of rotation (in or out of the page, your thumb points in the direction of the axial load $W_{xW}$)
• Also note that right handed worms that rotate out of the page pushes the thread to the left (or in the direction of $W_{xG}$)