Cash Flow Analysis

Summary

To compare and analyze cash flows we need to use common pattern of cash flows and functions to obtain equivalent cash flows. Use compound interest factors in this case which are formulas that define mathematical equivalence for specific common cash flow patterns. You can use tables instead of calculations assuming all periods are of an equal length and all cash flows and compounding occur at the end of each period.

Single Dispersion

Compound interest factor for single disbursement with interest rate i per period still uses $F=P{\left(1+i\right)}^n$ but instead of calculating our future value with this, we can use the tables to find the $\frac{F}{P}$ factor using n for a given interest rate, and then multiply our current value by that equivalent rate.

Equivalent time

Remember to do our time transformation here, for example, for an n=15, if we compound annually, our effective n is now 30. We need to also make the equivalent transformation on our interest rate.

Compound Interest Rate for Annuities

Instead of multiple instances per period, we can diagram our cash flow as a series…

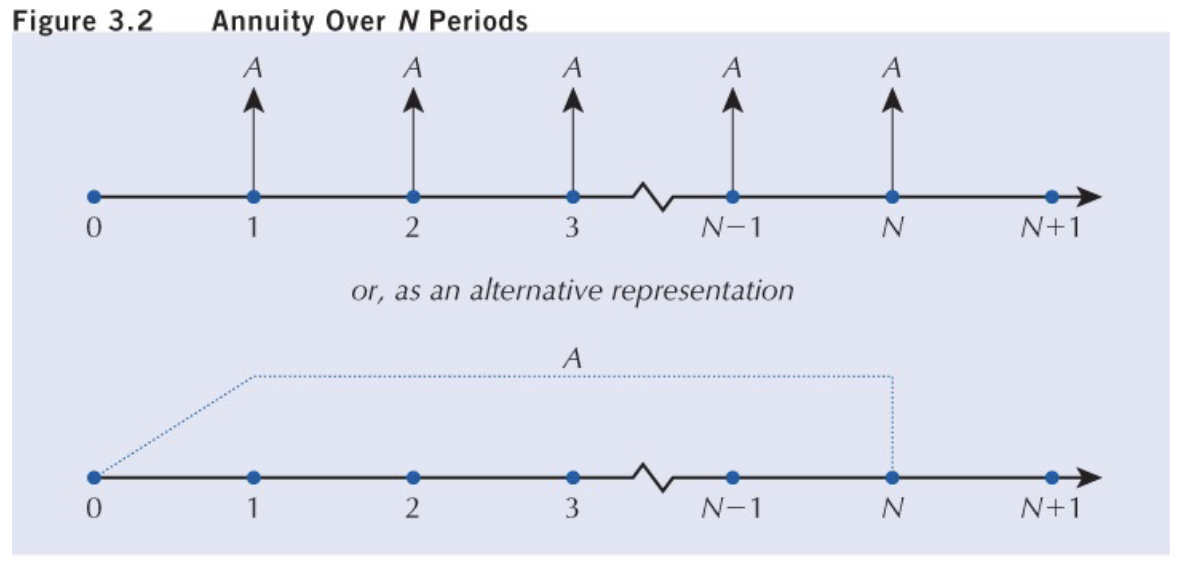
We have the following factors in our equivalent cash flows considering annuities…

• The uniform series compound factor (an equivalent future value of a series of equal cash flows over n periods) $\left(\frac{F}{A},i,n\right)=\frac{{\left(1+i\right)}^n-1}{i}$
• Sinking fund factor (a distribution which is equivalent to some future amount) $\left(\frac{A}{F},i,n\right)=\frac{i}{{\left(1+i\right)}^n-1}$

Using these factors

These factors make life easier when it comes to comparing values at different times as what is done in Equivalence Analysis. We basically do the same thing except we multiply each value by the $\frac{P}{A}$ factor at a given interest rate. If we are making a future value equivalent later down the line, we also need to multiply that term by a $\frac{P}{F}$ factor to normalize it to the beginning of our time line where we are taking things equivalent from.

Capital Recovery

Equivalent annual worth set equal to zero to find annual revenue that recovers capital cost

$AW=P\left(\frac{A}{P},i,n\right)-S\left(\frac{A}{F},i,n\right)$
Here:

• A is the minimum amount of income to recovery the capital cost
• S is the Salvage value defined in Time Value of Money If…
• Annual Income $>A$: Money made
• Annual Income $=A$: Covered costs
• Annual Income $<A$: Loosing money

To find what your equivalent annual worth is…

• $A=\left(P-S\right)\left(\frac{A}{P},i,n\right)+Si$

Conversion Factor for Arithmetic Gradient Series

Recognization

This is a series of receipts (+) or disbursements (-) that start at zero at the end of period 1 and increases (decreases) by a constant amount (G) from period to period. I.e, if you decrease by 200, then 220, 240, 260, etc..

We have the Annuity part which is a rectangle at the base, and then the G part which is the triangular part which grows in the cash flow diagram.

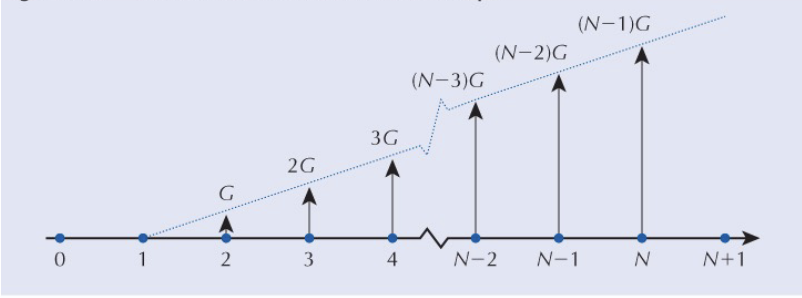
This conversion factor is…

• $\left(\frac{A}{G},i,n\right)=\frac{1}{i}-\frac{n}{{\left(1+i\right)}^n-1}$
• When you have a base annuity…
  • $A_{total}-A^{\prime }+G\left(\frac{A}{G},i,n\right)$
  • $P=A_{total}=\left(\frac{P}{A},i,n\right)$

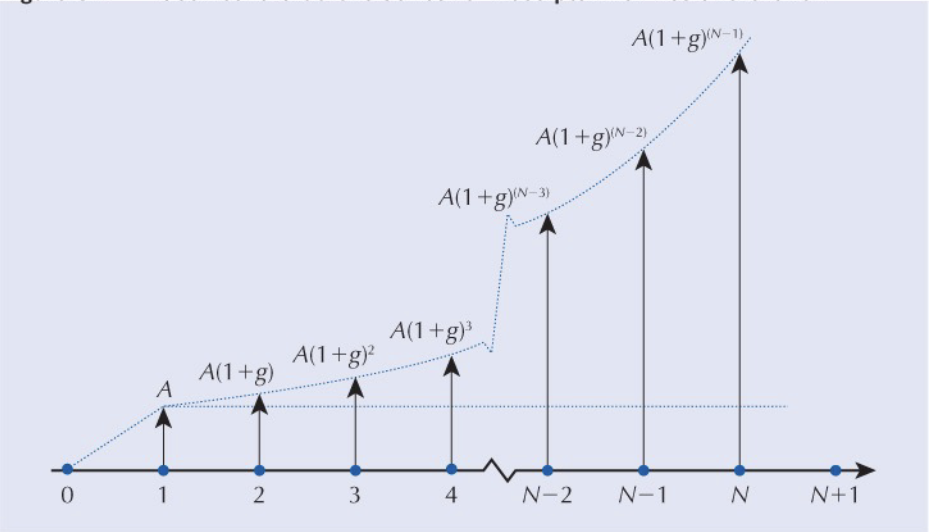
Conversion Factor for Geometric Gradient Series

Recognition

Instead of increasing by a constant rate, we increase by a constant rate (like 10%). Otherwise the same as the arithmetic gradient series.

The present worth of this series is…

• $P=\frac{A}{1+i}+\frac{A\left(1+g\right)}{{\left(1+i\right)}^2}\dots +\frac{A{\left(1+g\right)}^{N-1}}{{\left(1+i\right)}^N}$

By defining a growth adjusted interest rate ($i^0$):

• $i^0=\frac{1+i}{1+g}-1,\frac{1}{1+i^0}=\frac{1+g}{1+i}$
• The adjusted interest rate can be used to compute the equivalent present worth of a geometric gradient series like this…
  • $\left(\frac{P}{A},g,i,N\right)=\frac{{\left(1+i^0\right)}^N-1}{i^0{\left(1+i^0\right)}^N}\left(\frac{1}{1+g}\right)=\frac{\left(\frac{P}{A},i^0,N\right)}{1+g}$ If…
• $i>g>0\to i^0$: both tables and formula can be used
• $g>i>0\to i^0<0$: compute the conversion factor directly by formula
• $g=i>0\to i^0=0\to P=N\left(\frac{A}{1+g}\right)$ (use the P equation here)
• $g<0\to i^0>0$: both tables and formulas can be used

Present Worth when N → $\infty$

• Used for long lived projects
• $P={\lim }_{N\to \infty }A\left(\frac{P}{A},i,N\right)=A{\lim }_{N\to \infty }\left(\frac{{\left(1+i\right)}^N-1}{i{\left(1+i\right)}^N}\right)$
  • But this actually just means $P=\frac{A}{i}$

Non-Standard Annuity

Obtaining Present Worth
We use an $\frac{A}{F}$ factor to convert a series or single disbursement to year 1 to standardize them.

Example

For example, if we have a series of non-standard annuities that we want the present value of, we can do the following…

$P=1000\left(\frac{A}{F},i,4\right)\left(\frac{P}{A},i,20\right)$

• Where 1000 is investment value of the series
• 4 is the year of the first investment
• 20 is the year of the last investment.

The second term is the time discount.

You can use this for when annuities are not at year 0

Useful Formulas for Discrete Models