Financial Comparison Methods

Common Comparison Methods

• Present Worth (PW)
• Future Worth (FW)
• Annual Worth (AW)
• Payback Periods

The Assumptions Regarding Comparison

• Cost/Benefits are always measurable in terms of money
• Future cash flows are known with certainty
• Cash flows are unaffected by inflation or deflation
• Sufficient funds are available to implement all projects
• Taxes are not applicable
• All investments have a cash outflow at the start
  • These are first costs and the initial investment

Minimum Acceptable Rate of Return (MARR)

• Investing in a project means you cant invest the money anywhere else
• Therefore, MARR is an opportunity cost
• The MARR is the interest rate required for any project to be accepted

Present Worth

• All costs will be considered as negative values and incomes as positive
• Convert all cash flows to present time to calculate the Newt Present Worth (NPW) at MARR
• Then you can compare opportunities based on net profits, or least cost
• In this case:
  • The useful lives of alternatives are equal
  • The useful lives of alternatives are not equal

Equal Useful Lives

You maximize or minimize depending on the criteria considering profits or costs

• We calculate Net Present Worth by: $NPW=P{W}_{benefits}-P{W}_{\cos ts}$
• Then we choose the alternative with the higher NPW

Unequal Useful Lives

When making PW comparisons, the same period must be used to account for full costs/benefits. If the service lives are unequal we transform them into equal lives…

Repeated Lives Approach:

• Repeat the service life of each alternative over the least common multiple of service lives
• For a given cash flow, we literally repeat the single disbursement costs / receipts (except things that happen in the next n service lives need to be time shifted using (P/F, i, N) factors) where the repeating costs just have an adjusted N for the new life cycle usuing usually a (P/A, i, N) factor

Study Period Approach:

• Adopt specified analysis period for comparison
• Basically like the repeated lives approach except this is usually less than a service life and we have some sort of agreed upon salvage value at the end of the study period which is usually multiplied by a time shifting (P/F, i, N) factor
• We usually pick the shortest service life for the study period and adjust the larger one with a salvage value

Capitalized Cost

• The present sum that is required to provide the service indefinitely
• $P=\frac{A}{i}$

Future Worth

• We can choose between alternatives by finding their equivalent value at some given future date

Annual Worth

• Basically the same as PW except all disbursements and receipts are transformed into a uniform series at MARR
• AW comparisons may be easier to conceptualize than PW (annual cost to operate your car for example)
• For two things with the same life, PW and AW are basically the same
• You can choose which method of comparison to use based off of physical meaning and what makes sense with your audience
• Any present worth P can be converted to an annuity A by the capital recovery factor (A/P,i,N)
• Even though the method is called annual worth, the uniform series is not necessarily on a yearly basis

Annual Cash Flow Analysis

• Use if two strategies yield the same benefits, we should choose the one with the lower equivalent annual costs in this case
• Similarly, if two strategies have the same costs, we choose the one with the higher equivalent annual benefits in this case
• If the lives are equal, the analysis period is based on the same lifetime
• If the lives are unequal, the analysis period is based on alternate lifetimes.
  • No LCM is required as in present worth analysis
  • Multiples of service lives are equivalent to one service life with annual worth analysis -therefore, it doesn’t matter here!
• Here we just use (A/P, i, N) for whatever the service life is and we are good to go assuming that it is possible for alternatives to be repeated
  • Else, we need to use a study period which uses (P/A, i, N)

Infinite Life

For example, if we have one alternative with infinite life, we need to use this method

And we can also use… $A=Pi$ for things of an infinite life

Payback Periods

• The number of years it takes for an investment to be recouped (interest assumed 0)
• If annual savings are constant then…
  • Payback period $=\frac{\text{First Cost}}{\text{Annual Savings}}$
• If they are not constant, we deduct each year of savings from the first cost until the first cost is recovered
  • Here, the project with the shorter payback period wins
  • Usually a payback period of 2 is acceptable where 4+ is bad
  • This is simply a heuristic

Internal Rate of Return (IRR)

• A projects rate of return is defined by the IRR
• The Interest rate at which the present worth and equivalent uniform annual worth are equal to zero
• This is when the benefits = the costs
• Given a cash flow, there are 5 forms of equations that we can use to solve for an unknown interest rate…
  • Net present worth = 0
  • PW of benefits = PW of costs
  • PW of benefits/PW of costs = 1
  • EUAB = EUAC
  • FW of benefits = FW of costs

IRR vs ERR

IRR is the RoR for an individual project,
ERR is for when the IRR doesn’t exist as an individual value (more than 1 root for the equation PW = 0 for some unknown interest rate))

Essentially, $PW=0$ for some unknown i, where i is the RoR or the IRR when our present worth is = 0…

If only one solution exists to this relationship, then the obtained i is our IRR
If the solution has more than one root (multiple values of i), then one is the IRR and one is the ERR?

• Assume we are obtaining the IRR for an individual project
  • → If IRR ≥ MARR → the project is justified, else it isn’t justified for an investment

Deception

Note that the IRR can be deceiving, our goal is to maximize our money (PW, AW, etc) not our rate of return sometimes the higher IRR will not yield the more profitable investment depending on cost and the amount allowed to be invested

Incremental Analysis

• Two or more alternatives are compared using their $\Delta IRR=IR{R}_A-IR{R}_B$
• Steps
• The project increment is ordered by… higher cost → lower cost
• Consider the difference of incremental investments then obtain their IRRs
• If $\Delta IRR$ > MARR
  • Then this increment is justified from the option with higher initial cost
• Otherwise, the increment is not justified and the cheaper option is the choice
• The opposite is true from the borrowing perspective
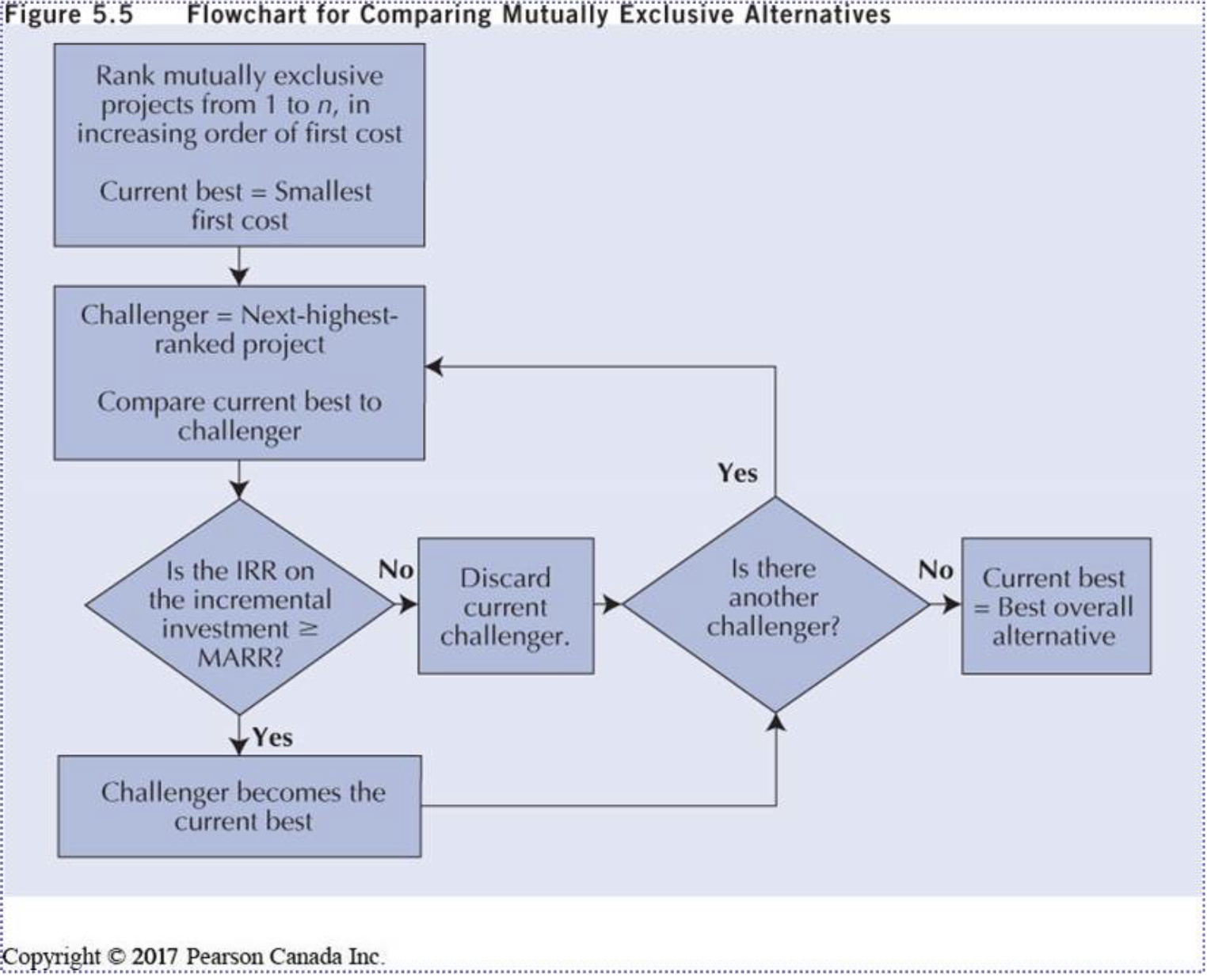
• The IRR Algorithm
  • Calculate the RoR for each alternative and discard any for IRR < MARR
  • Arrange the remaining alternatives in ascending order of first cost
  • The alternatives with the lowest first cost is the current best
  • Calculate the incremental IRR of upgrading the current best to the next lowest cost alternative
  • If the incremental IRR > MARR, replace your current IRR
• Here an increment, is just the next alternative

• Like the PW, or FW methods, we need to have equal lives for $\Delta IRR$ as well (we need to normalize the service lives)
  • We can use LCM or Study Period Analysis here

External Rate of Return

• The IRR is determined by the cash flows of a given project and solving for the roots
• Denoted by $i_e^{\ast }$, this is the rate of return where any excess cash earns interest at an explicit rate which is usually the MARR
• This is any received money that is not required for the current project at that time will be invested elsewhere with MARR until needed for the project

Steps

1. Convert all inflows (receipts) to a future value at the MARR and call it FWB(MARR)
2. Convert all costs (cash outflows) to a future value at n with an unknown interest rate $i_{ea}^{\ast }$ and call it FWC($i_{ea}^{\ast }$)
3. Solve the equation of FWB(MARR) = FWC($i_{ea}^{\ast }$) for $i_{ea}^{\ast }$

• We use the ERR whenever multiple IRR’s are possible (multiple roots to an i for IRR) where we would get these i’s using the IRR() function in excel