Uncertainty and Risk

• Most economic evaluations involve estimating project parameters (prices, interest rates, timing, etc)
• Sensitivity analysis gives a better understanding on how uncertainty affects the outcome of the evaluation
  • Here examine sensitivity of performance measures to changes in the values of uncertain parameters

Some Sensitivity Analysis Methods Include

Sensitivity Graphs

• Illustrate sensitivity of performance measures (like PW, AW) to changes in parameters Decision Trees
• Use probabilistic information to vary input variables to understand how much a final decision or outcome changes identifying which inputs are the most critical Break-even Analysis
• Answers the question “what production level is necessary for PW ≥ 0”
• We basically solve the above equation Principles of Probability
• Helps to understand risk

Sensitivity Graph Analysis

• Obtain the PW of the project based on estimated values for parameters (capital cost, O&M costs, salvage price, savings/benefits/incomes, and interest rate) as the base case
• Then, at each run, assume one parameter changes while keeping others constant at their base level
• Typical range for change in values: -10%, -5%, +5%, +10%
• Graph the PW on the change of each parameter
• We need to do this in excel since there are many cases that we need to consider
• Then we graph PW vs the parameter change which generates a graph like this…

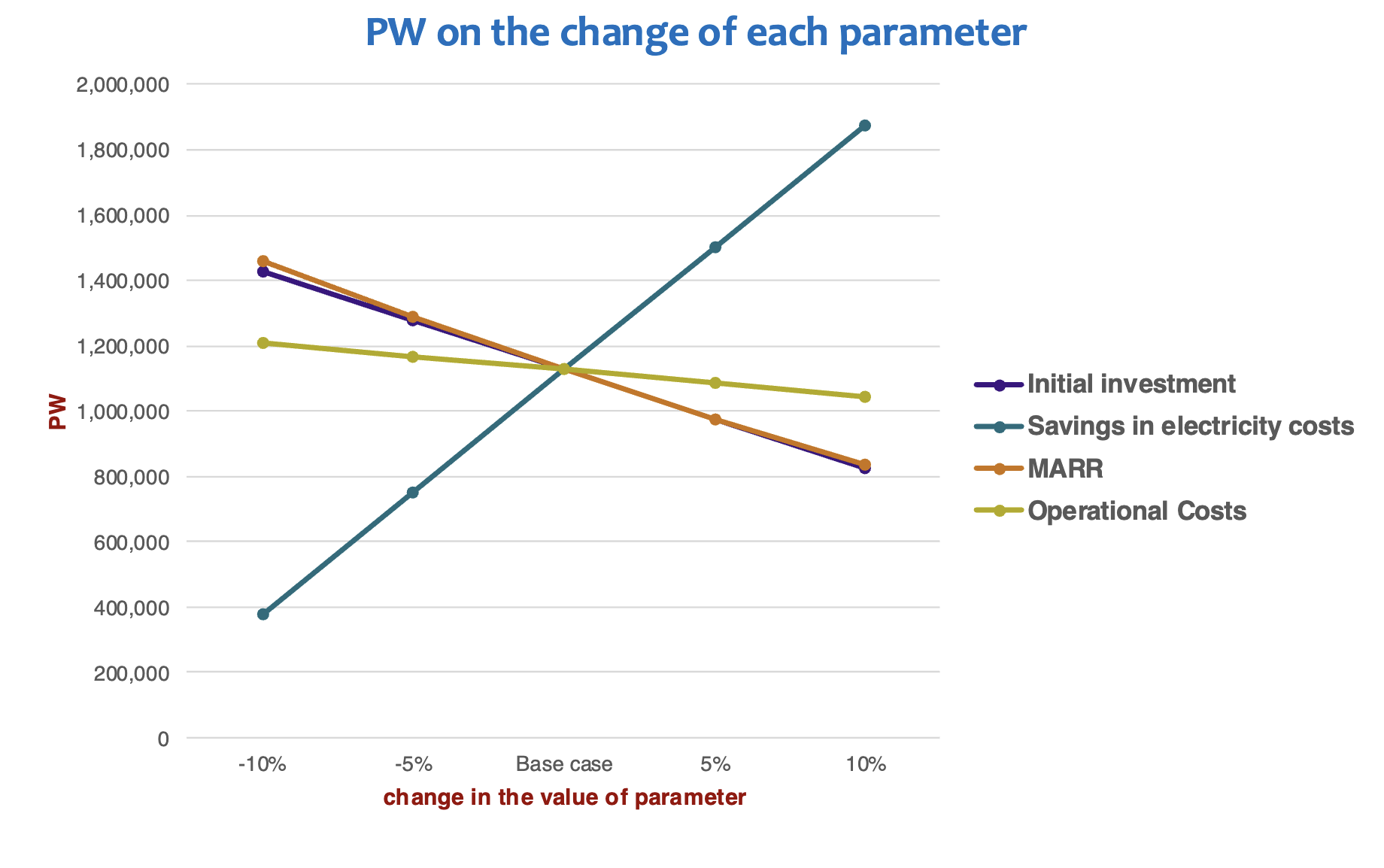
Decision Trees

• Formal methods aid engineers in evaluating complex problems under uncertainty / risk:
  • Provides means of decomposing a large problem and structuring it into sequence of smaller components
  • Suggests a variety of decision criteria to help with the process of selecting a preferred course of action
  • Provides a graphical means of structuring where uncertainties are characterized by probability distributions
  • Clarifies options decision maker has / provides framework with which to deal with the risk involved

There are four main components in a decision tree:

1. Decision node: Represents a decision to be made by the decision maker – denoted by a square
2. Chance node: Represents an event whose outcome is uncertain – denoted by a circle
3. Branches: Connect nodes from left to right, depicting the sequence of possible decisions and chance events
4. Leaves: Indicate the values, or payoffs, associated with each terminal (rightmost) branch of the tree A decision tree grows from left to right, illustrating the flow of decision-making and uncertainty

To Analyze the Tree:

1. Start from the leaves and move backwards to the left
2. At any chance node, calculate the EV and put the value on the chance node
3. At any decision mode, make a decision based on values and criterion for decision making and terminate the unchosen decisions by “//” and put the value of decision on the decision node
4. Continue until the root node is reached

Note

• Whenever a chance node follows a decision node, it implies that the decision maker must anticipate the outcome of future uncertain events in decision making.
• When a decision node follows a chance node, it implies that a decision must be made assuming that a particular outcome of a chance event has occurred.