Loop Shaping

For a general feedback control system…

There are fundamental tradeoffs due to $S\left(s\right)+T(s)=1$ We need…

• For tracking, parameter uncertainty, disturbance rejection… S(s) to be small → $G_K{G}_P$ is large
• For noise rejection, parameter uncertainty… T(s) to be small → $G_K{G}_P$ is small The main idea of loop sharing is to design the controller $G_K\left(s\right)$ such that these FR (frequency responses) can be shaped to a desired form.
  Fortunately…
• Reference ($R\left(s\right)$), disturbance ($D\left(s\right)$), and some parameter uncertainties usually have low frequency contents
• Noise ($V\left(s\right)$) and other parameter uncertainties have high frequency contents Therefore, we can make $|G\left(j\omega \right)|$ large for low frequencies and small for high frequencies!

Stability Margins

For stability we need to avoid $G\left(s\right)=-1$ for any Re(s) > 0…
In other words, we don’t want $|G\left(s\right)|=-1$ or $<G(j\omega )=-180°$ for $\omega >0$…
This is why we need $GM>0$ and $PM>0$!

The main idea is…
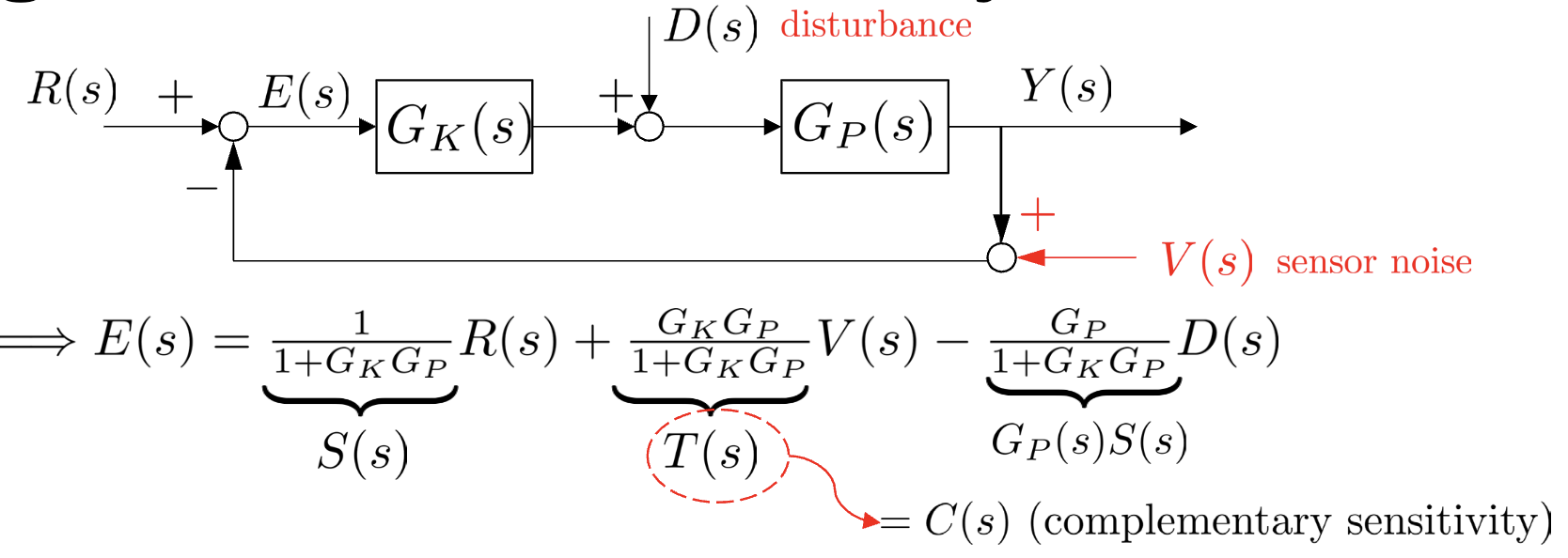
We can design $G_K\left(s\right)$ to shape the loop function $G\left(s\right)$ as desired over all frequencies, bode plots and their additivity are key tools here…

We can basically just use superposition here to get our desired shape!

What are good shapes?

• Positive phase in $(G_K(j\omega )$ can increase PM of $(G(j\omega ))$
  • e.g. PD control $(G_K(s)=K_P\left(\frac{s}{T}+1\right))$
  • Or stabilize it if PM of $(G_P(j\omega )<0)$
• Squashing high frequencies reduces effect of noise.
• Infinite gain at $(\omega =0)$ reduces the steady-state errors, e.g. PI control $G_K=\frac{K_I}{s}\left(\frac{s}{T}+1\right)$
• Large closed-loop bandwidth is equivalent to large cross-over frequency (for faster response speed).
• Achieving these in frequency domain (i.e., Bode shapes) can often be a bit tricky (tuning is a bit of an art).

Lead and Lag Compensation

PD Compensation: $G_K\left(s\right)=K{D}_C\left(s\right)$ with $D_C\left(s\right)=T_{D}s+1$

• We have a stabilizing effect if we have a positive slope (+1), and positive phase $<D_C\left(j\omega \right)\ge 45°$ at $\omega >\frac{1}{T_D}$
• We have increased magnitudes at high frequencies → may amplify high frequency noises…
  • This is not desirable since we want to suppress our magnitudes at high frequencies, this is the trade-off…

Instead of using PD compensation, we use lead compensation which is a generalized version of PD compensation…

• To alleviate that high frequency amplification, we add a pole at $\omega >\frac{1}{T_D}$
• This is what lead compensation is… $D_C\left(s\right)=\frac{T_{D}s+1}{\alpha T_{D}s+1}=\frac{1}{\alpha }\frac{s+\frac{1}{T_D}}{s+\frac{1}{\alpha T_D}}$ where $\alpha <1$
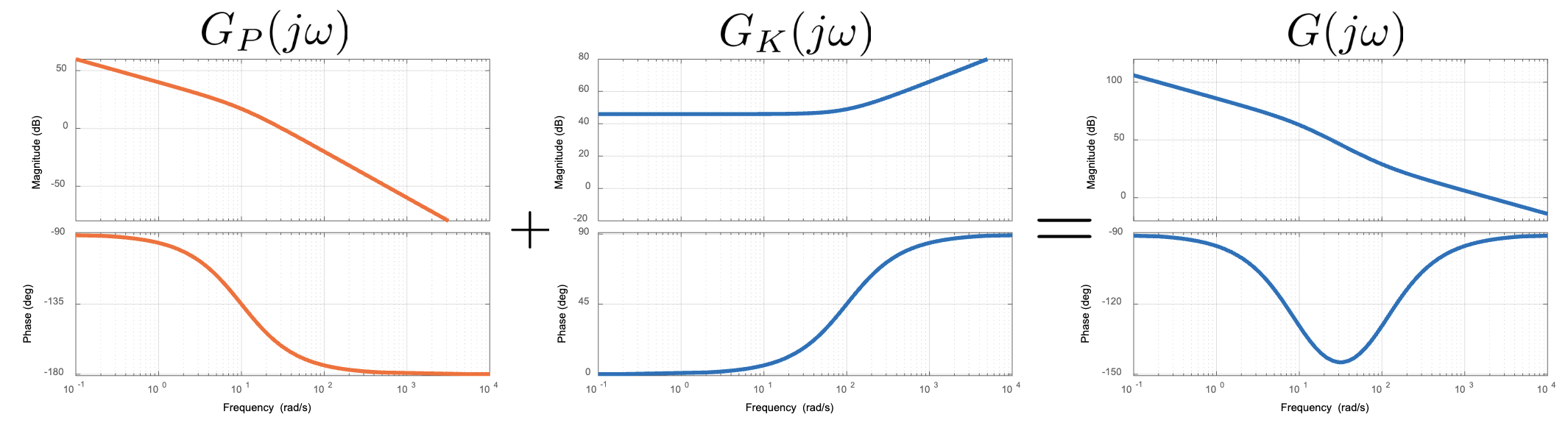
• Some key points of phase and magnitude include
  • $\varphi \left(\omega \right)={\tan }^{-1}\left(T_D\omega \right)-{\tan }^{-1}\left(\alpha T_D\omega \right)$ with ${\omega }_{\max }=\frac{1}{T_D\sqrt{\alpha }}$ and $\sin {\varphi }_{\max }=\frac{1-\alpha }{1+\alpha }$
  • Another property is $\log {\omega }_{\max }=\frac{1}{2}\left(\log \left(\frac{1}{T_D}\right)+\log \left(\frac{1}{\alpha T_D}\right)\right)$ where the first log term is the zero, and the inside of the second log term is the corresponding zero

General Guidelines for Lead Compensation

• Choose ${\varphi }_{\max }$ to be a bit bigger than needed for PM (phase-margin)
• $\alpha$ can be chosen based on by how much PM we need to increase using $\sin {\varphi }_{\max }=\frac{1-\alpha }{1+\alpha }$
• Choose $T_D$ (zero-location) appropriately so that the ${\varphi }_{\max }$ occurs at the crossover frequency ${\omega }_c$ noting the value of $\log {\omega }_{\max }$ General Procedure
• Determine $K$
  • To meet $e_{ss}$ requirement
  • To meet ${\omega }_{BW}$ requirement (pick $K$ to make $2{\omega }_c={\omega }_{BW}$)
• Check PM for chosen K and allow for a buffer of 10°-20° to determine the required lead phase ${\varphi }_{\max }$
• Determine $\alpha$ based on ${\varphi }_{\max }$ using (${\varphi }_{\max }$ - $\alpha$ plot)
• Pick ${\omega }_{\max }$ to be at the cross-over frequency by ${\omega }_{\max }=\frac{1}{T_D\sqrt{\alpha }}$
  • $\log {\omega }_{\max }=\frac{1}{2}\left(\log \left(\frac{1}{T_D}\right)+\log \left(\frac{1}{\alpha T_D}\right)\right)$
• Draw Bode plot to check
• Iterate as needed

PI Compensation

$G_K\left(s\right)=K{D}_C$ with $D_C=\frac{1}{s}\left(s+\frac{1}{T}\right)$

• Tracking effect: infinite gain at $\omega =0$
• Decreased phase at frequencies lower than ${\omega }_c$ may degrade stability by decreasing $PM$ for $\omega <\frac{1}{T}$

Lag Compensation

To alleviate low frequency phase decreases, add a pole at $\omega <\frac{1}{T_D}$

• This is called lag compensation $D_C\left(s\right)=\alpha \frac{T_{I}s+1}{\alpha T_{I}s+1}$ where $\alpha >1$
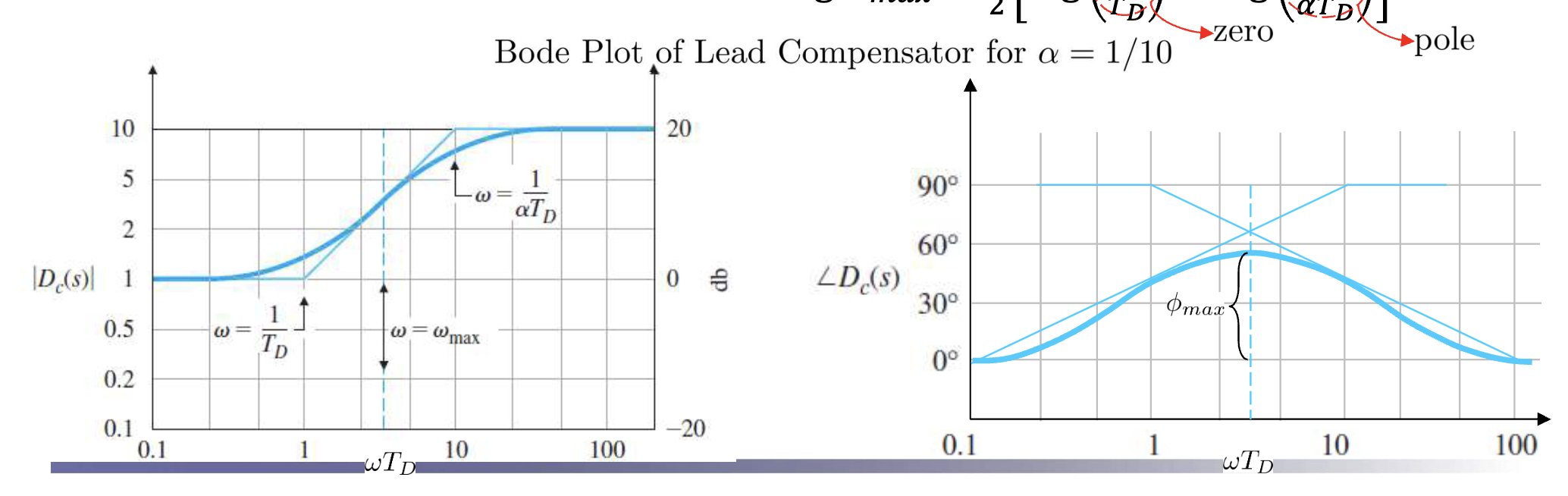
• Key properties of the magnitude and phase…
  • Increase in amplitude at low frequencies
  • Increase in phase at low frequencies General Procedure
• Determine $K$ to meet required PM w/o compensation
• Draw Bode plot to evaluate low-frequency gain
• Determine $\alpha$ for the low-freq. gain requirement (e.g. $K_P$) where $\alpha$ is based on the chosen value of $K$ and what $K$ should be ($K_p=\alpha K$)
• Choose the corner frequency $\omega$ = $\frac{1}{T_I}$ (the zero) to be 1/2 ~1/10 below the new ${\omega }_c$
• The other corner frequency is then $\omega =\frac{1}{\alpha T_I}$
• Iterate as needed

Some guidelines

Lead compensator for PD, Lag compensator is for PI

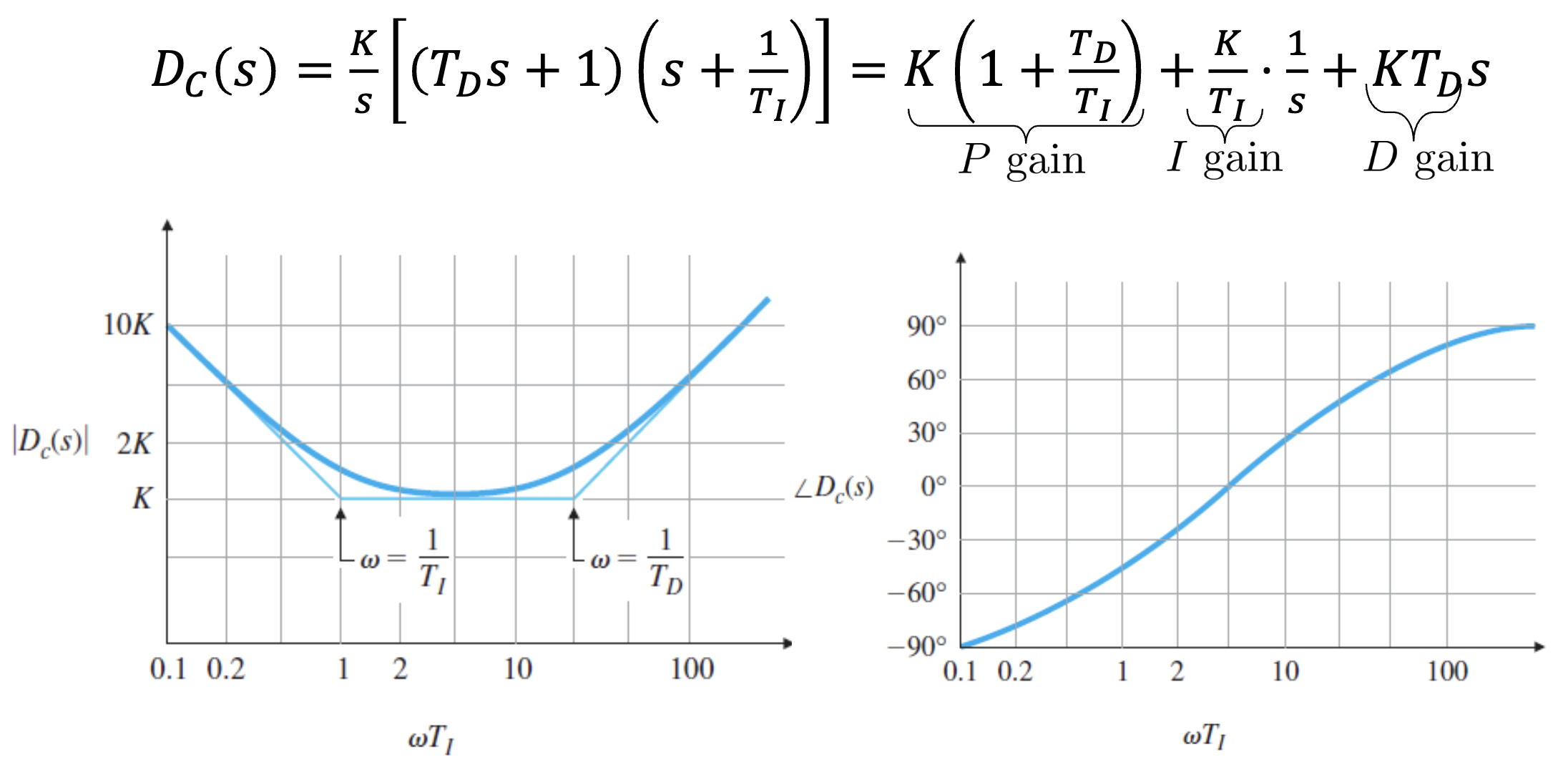
We can use PID compensation to achieve PM improvement at ${\omega }_c$ and low frequency gain improvements

Notch Compensation

• Instead of damping control like PD, we can specifically target the resonance frequency to cancel it out
• This only works if the oscillation frequency is well known and does not change with time
• Typically of the form $G_{\text{notch}}=\frac{s^2+2\zeta {\omega }_{n}s+{\omega }_n^2}{s^2+2{\omega }_{n}s+{\omega }_n^2}$
• The lightly damped poles can never be fully canceled
• Nevertheless, it can suppress them in a targeted way
• Loop TF: $G=G_{\text{notch}}{G}_p$