Control Volumes

What even is this?

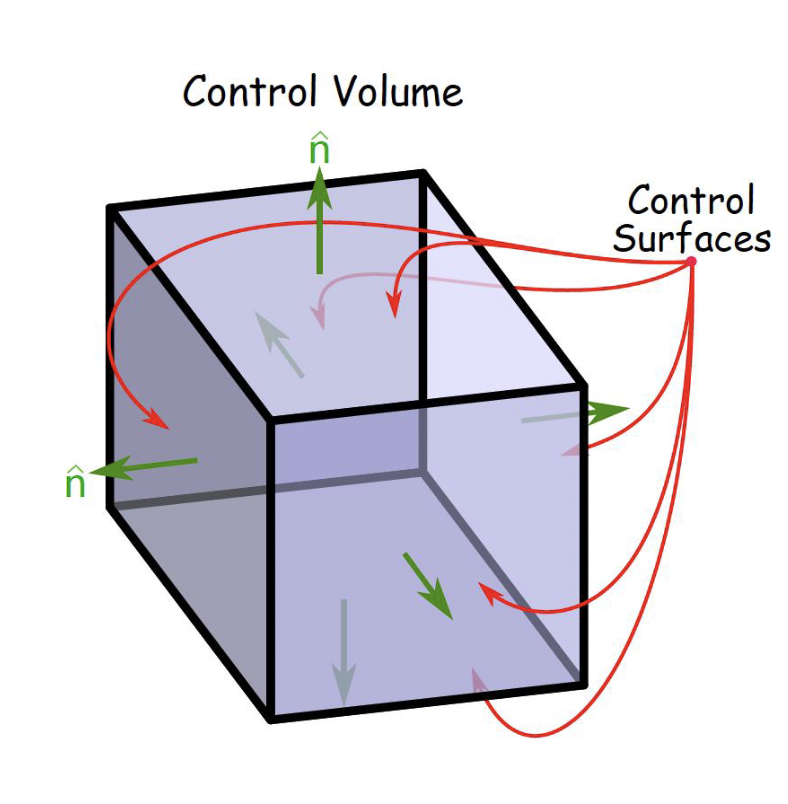
• A clearly defined closed region in space
• Surfaces of a control volume are control surfaces
• Unit vector normal to control surface, n, is always directed outward
• We formulate equations as balance equations that apply over a given region of space or formulate equations (mass, momentum) that apply at each point in space

What is it actually

A control volume is a mental boundary that we define so that we can write conservation equations for mass and momentum, this is the same as defining our system in Thermodynamic Basics (Systems and Properties)

Why?

We use control volumes to look at conservations laws… The three ones related to fluid mechanics are…

• Conservation of mass
• Conservation of linear momentum
• Conservation of energy

This is intuitive for a system with many components

Differential form of conservation laws

• $\frac{1}{V}\frac{dV}{dt}=\frac{du}{dx}+\frac{dv}{dy}+\frac{dw}{dx}=0\cong \rho \frac{dV}{dt}=0$ when p is const

We can use the idea of control volumes kind of like how we interact with circuits

How to choose the control volume

• It should contain the region of interest
• Boundaries should be placed where the information is known
• It can be of arbitrary shape
• It can move or deform
• In ME351, our control volumes will be fixed in shape and stationary or moving at a constant velocity

For Generic Control Volumes

• Only normal components contribute to an inflow or an outflow

Processes Associated with a Control Volume

• Storage or accumulation
• Inflow / outflow across control surfaces

How Do we Actually Obtain a Conservation Equation?

Storage

• RoC of mass in control volume ($CV$)
• $\frac{d}{dt}\int \int \int pdV$ Flow
• In flow and outflow through out control surfaces
• $\int \int \varrho \left(Vn\right)dA$ Putting it together…
• $\frac{d}{dt}\int \int \int \varrho dV+\int \int \varrho \left(V\cdot n\right)dA=0$
• This is our scalar equation for conservation of mass

Control volume formulation of conservation laws

1. Define control volume
2. Draw normals
3. Identify processes

Conservation of mass…

• $\frac{d}{dt}\left(pdv\right)+\left(p\cdot v\cdot dA\right)+\left(p\cdot v\cdot dA\right)=0$ where this is storage + inflow + outflow = 0
• The 1D flow assumption is more valid at turbulent flows (more common)

Vertical water jet example

• Select a control volume and justify your choice
• Assume
  • 1D at in/out
  • Steady
  • P=const
  • Incompressible
• No mass stored in the control volume since “steady” was an assumption = 0 = $m_{in}^{\prime }-m_{out}^{\prime }$
• $p{V}_{in}{A}_{in}=p{V}_{out}{A}_{out}$
• When you have a boundary layer, you need to integrate to ${\partial }_l+{\partial }^{\ast }$

Finding U_{\max}

• Given a circular pipe cross section…
• We have the directions of flow of $V_{in}$ and $V_{out}$ as well as the directions of their normals (both out of the tubes)
• Assuming:
  • Steady
  • $p$ = const
  • 1D inlet
• Use conservation of mass equations

Cylindrical Containers

• $pA\frac{dh}{dt}=-p{V}_{out}{A}_{out}$
• Now we can use this to solve for the unknown (sometimes diameter)

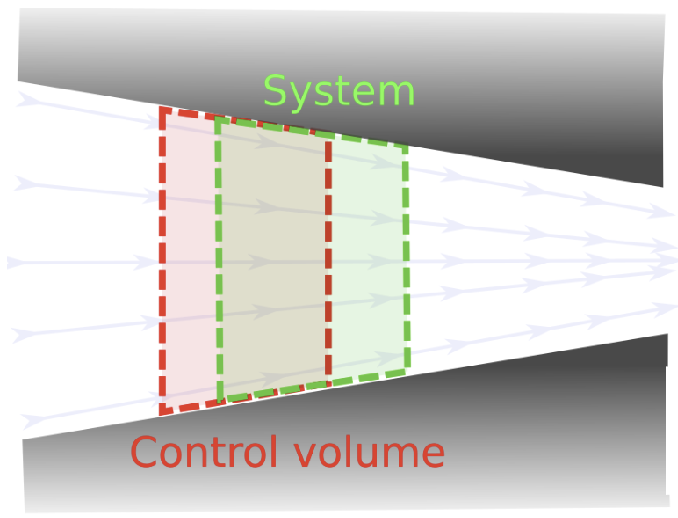
Systems and Control Volumes

At t=0, the system and control volumes are coincident

• At time t: $m_{sys}\left(t\right)=m_{cv}\left(t\right)$
• At time $t+\partial t$: $m_{sys}\left(t+\partial t\right)=m_{cv}\left(t+\partial t\right)-m_1\left(t+\partial t\right)+m_3\left(t+\partial t\right)$
• Where 1, 2, and 3 represent the control volume, the overlap, and the system here

Reynolds Transport Theorem
Here, $m_{sys}\left(t+\partial t\right)-m_{sys}\left(t\right)=m_{cv}\left(t+\partial t\right)-m_{cv}\left(t\right)-m1\left(t+\partial t\right)+m_3\left(t+\partial t\right)$

Conservation of Momentum

$\frac{d{N}_{sys}}{dt}=\frac{\partial }{\partial t}\int \int \int \varrho \eta dV+\int \int \varrho \eta V\cdot dA=\sum F$

• Where $N_{sys}$ is our extensive property and $\eta$ is our specific property
• The first term is our storage term and the second is the flux across the control surfaces
• This is also written as $\text{storage}-m^{\prime }{V}_{in}+m^{\prime }{V}_{out}=\sum F$

Cross Over

You can kind of see a relation between this and Mass and Energy for Open System from Thermo