Gears

Useful Equations and Properties of Gears

Pitch is given as $p=\frac{2\pi R_1}{N_1}=\frac{2\pi R_2}{N_2}$ Where N: number of teeth

Velocity is given as $v=R{\theta }_1^{\prime }=R{\theta }_2^{\prime }$

• Where no slipping is also assumed.
• Where ${\theta }^{\prime }$ = w (angular acceleration)

No power loss = no heat inertia or no acceleration and no friction loss gives us this condition

• $T_1{\theta }_1^{\prime }=T_2{\theta }_2^{\prime }$

In terms of work: $T_1{\theta }_1=T_2{\theta }_2$ where $\frac{{\theta }_2}{{\theta }_1}=\frac{T_1}{T_2}=\frac{N_2}{N_1}$

• Where N2/N1 is the gear ratio.

Note on gear ratios

If N2/N1 > 1 then w2 < w1 and T2 > T1 (speed reducer)

Equivalent Inertia

See Equivalent Mass and Inertia

---

Examining the effect of the system (shaft and gear)
We get T1 and T2 which are not the same but… $n_2{T}_{1G}=n_1{T}_{2g}$
Since there is no moment of inertia here

• $T_2-T_{2G}=0\ast {\theta }^{{}^{\prime \prime }}$
• $T_2=T_{2G}$
  And by using a previous equation
• $T_{1G}=\frac{n_1}{n_2}{T}_2$

---

Solving Gear Questions Tips

See my practice problems for a more detailed explanation

Key Points

When analyzing gear ratios:

• If you have a motor driving a gear train, the gear ratios applied to a gear are baed off of what the gear needs to drive from the motors perspective. For example, the gears on the same axel as a motor have the total equivalent gear ratio (product of N) because they still need to drive the entire system. The first intermediate gear however, will only have subsequent gear ratios not including the first one because the first gear ratio is accounted for by the gear it interacts with.
• You also need to find an equivalent torque by the whole gear train which is also done using gear ratios
• Use the axis of the output shaft as the neutral axis you take moments about

In terms of gears, Inertia is: $I^{\prime }=\frac{I^{}}{N}$ where I’ is the output inertia and I is in the input inertia

Torque of Gears Relationship

Power of a gear train is given by the very important equation…

• $P=\omega T=2\pi nT/60$
  • Find max torque to find max power where max torque is $T=W_t\cdot d$
• You can use something like $v=\pi d_p{n}_p$ to find pitch line velocity

Schematically

Gears are hatched in schematics

Types of Gears

• Spur
• Helical
• Straight bevel
• Spiral bevel
• Worm and worm gear pair
  • Accommodates self-locking (you can’t rotate the output shaft through the output shaft, only through the input shaft)

Gears

Gear Trains

Relevant Notes

Gear Train Analysis

• At the intersection of two gears, the tangential velocity is the same (i.e $v_1=v_2$ or ${\omega }_1{R}_1={\omega }_2{R}_2$) where you can use the equation at the beginning of this section.
• By using this relationship, we can find the rotational speeds (rpm) of the different gears using the gear ratios ($\frac{d_1}{d_2}$)

Planetary (Epicycle) Gears

• A type of gear train
• A 2 DOF gear
  • A sun gear, planet gear and ring gear
  • One of these gears need to be fixed
• Input and output can be coaxial (e.g automatic transmission)

Some Important Definitions

• Pinion: the smaller of two gears
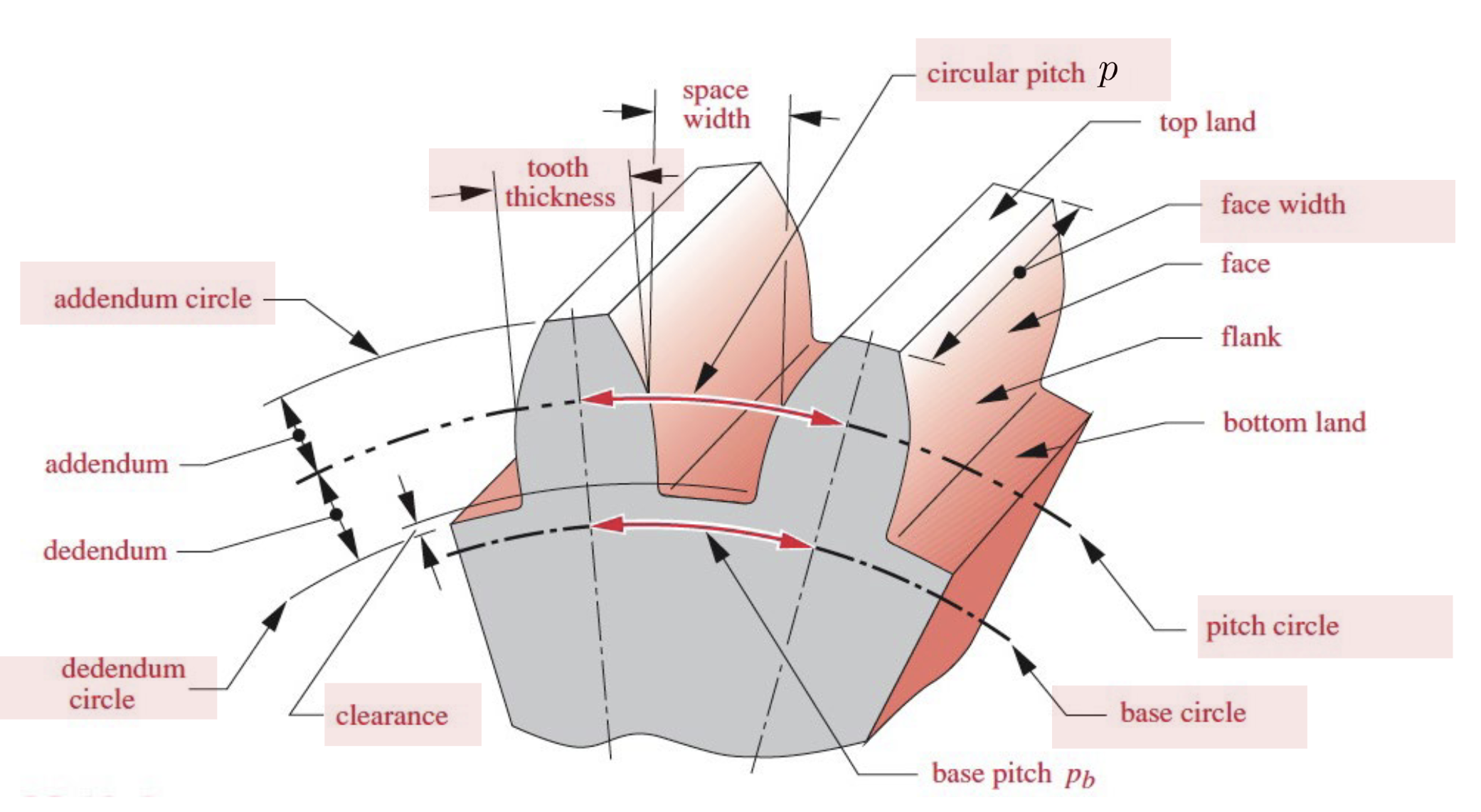
• Pitch circle: theoretical circle for all load analysis
• Pitch diameter: dia. of pitch circle
• Circular pitch $p=\frac{\pi d}{N}$
• Number of teeth $N$
• Module $m=\frac{d}{N}$ [mm]
• Diametral pitch $P=N/d$
• Gear ratio $\frac{N_g}{N_p}=\frac{d_g}{d_p}$
• Addendum $a=\frac{1}{P}$
• Dedendum $b=\frac{1.25}{P}$
• Cone distance (uses Pythagorean Theorem since this is the slant of the pitch cones for a 90° interface $A_o=\sqrt{{\frac{d_1}{2}}^2+{\frac{d_2}{2}}^2}$)
• P or m defines tooth size
• Mating gears need to have the same tooth size (module or dia. pitch)

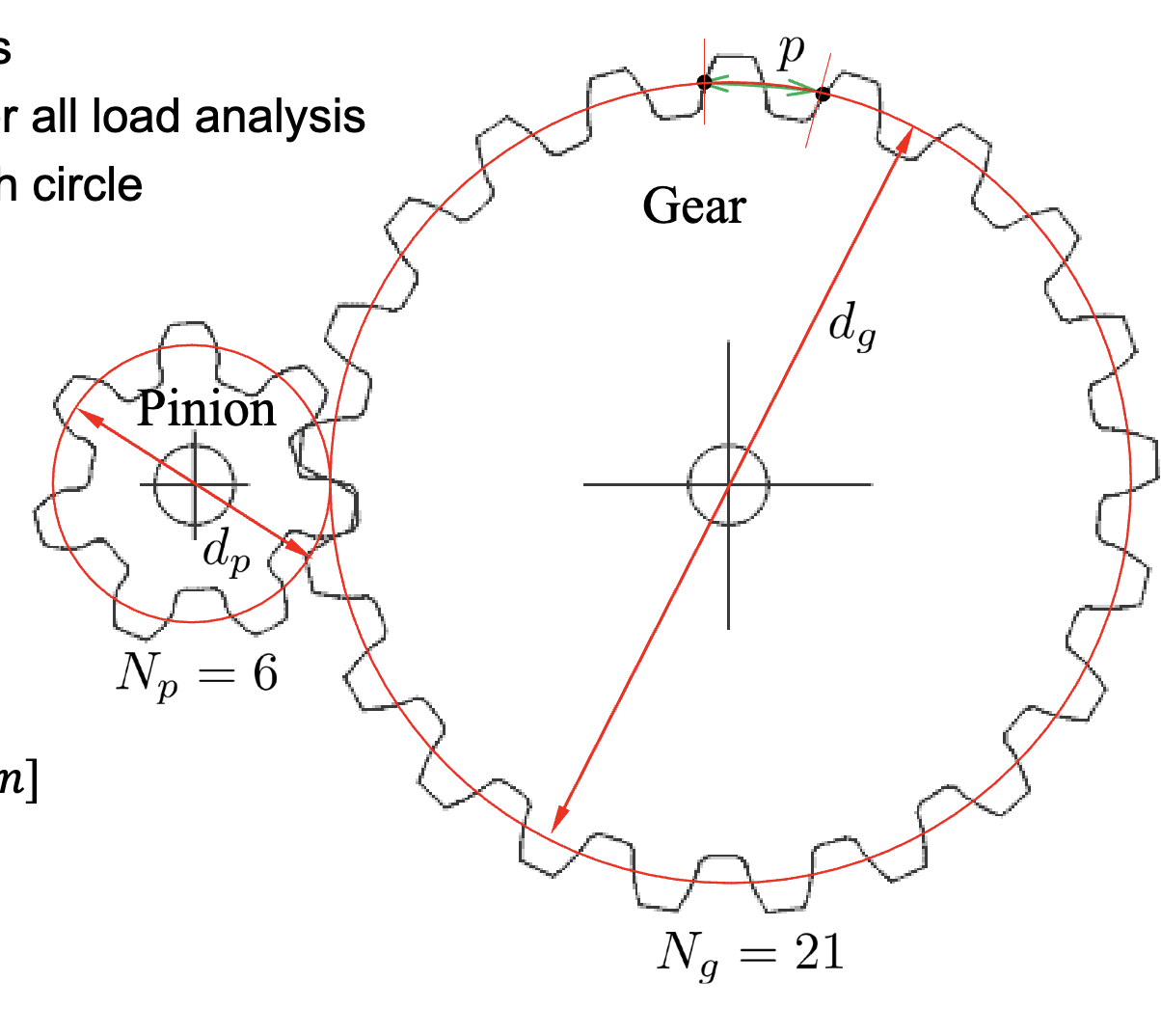
Terminology

Fundamental Law of Gearing

• Angular velocity ratio between the mating gears must constant throughout the mating of teeth
• Meshing gears need to be conjugate in design
  • To do so, the gear teeth need to be of a specific geometric shape
  • The involute teeth shape is the most widely used

Involute Tooth Form

• A curve generated by unwrapping a taut string from a cylinder
• The string is always tangent to the base circle
• The end of the string forms the involute curve which is the shape of the tooth
• The center or curvature of the involute is always at the point of tangency of the string with the base circle
• A tangent to the curve is always normal to the string which is the instantaneous radius of curvature of the curve
• The tangent at the point where the two teeth engage is the common tangent

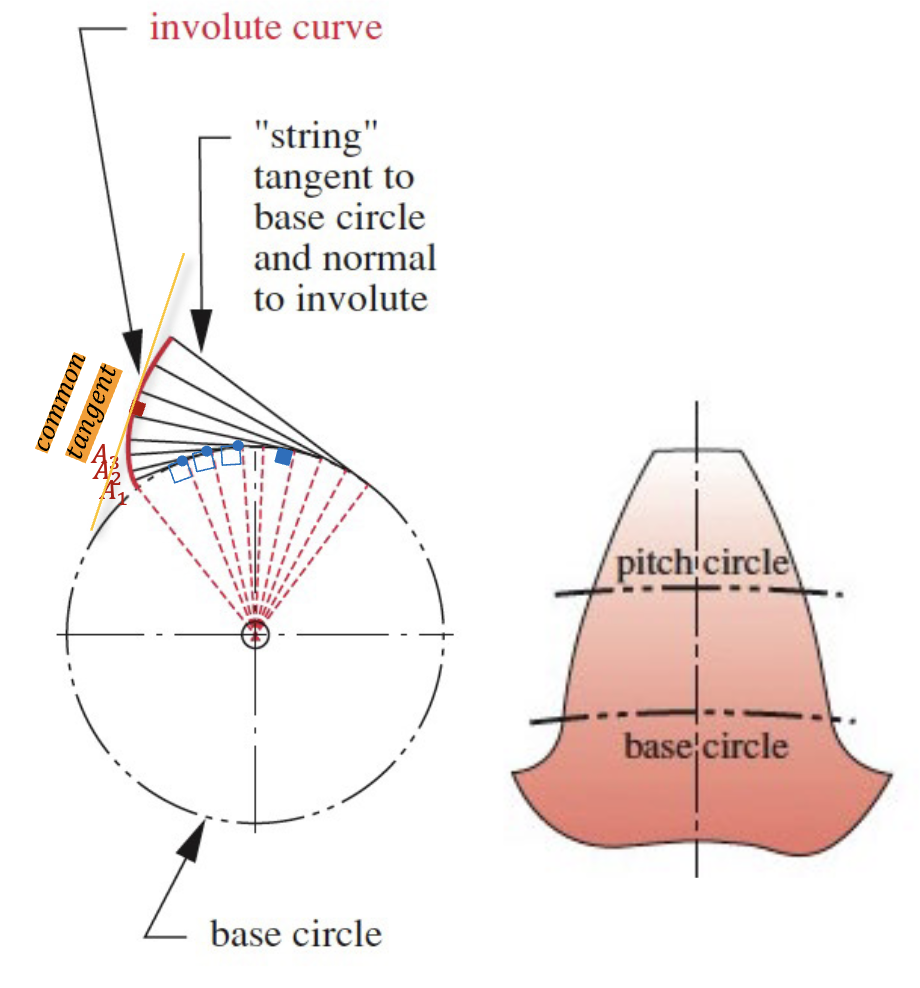
• This point of tangential load transfer is tangent to both teeth and has a pressure angle (of typically 20°)
  • Where you can form the following relationship $\cos \left(\varphi \right)=\left[\frac{r_{base}}{r_{pinion}}\right]$
• Another advantage is that the shift in center distance (alignment error) does not affect the gear ratio $\frac{r_g}{r_p}=\frac{\Delta r_g}{\Delta r_p}$ (MAIN PROPERTY) Interference
• Gear cutting tools remove interference areas which weakens the tooth (bad)
• You want to be in between case 1 and 2
• Case 1: Given a ratio $m_G=\frac{N_G}{N_P}$ the minimum number of pinion teeth needed to avoid interference is: $N_P=\frac{2}{(1+2m_G){\sin }^2\varphi }\left(m_G+\sqrt{m_G^2+(1+2m_G){\sin }^2\varphi }\right)$
• Case 2: Given $N_P$ the maximum number of gear teeth to avoid interference $N_G=\frac{N_P^2{\sin }^2\varphi -4}{4-2N_P{\sin }^2\varphi }$

Types of Gears

Spur Gears

See Spur Gears

Helical Gears

See Helical Gears

Bevel Gears

See Bevel Gears

Worm Gears

See Worm Gears

Solving Gears

• The key here is to draw a good and representative FBD in all planes of action
• When we have screws on a rotating shaft, they resist the motion of the rotating shaft (the direction of the moment)
  • We get the direction of these moments from how $W_t$ and $W_r$ rotate their respective axis

We select gears using this criteria Gears