Bernoulli's Principle

Use when you have pressure and want a velocity or the other way around!!!

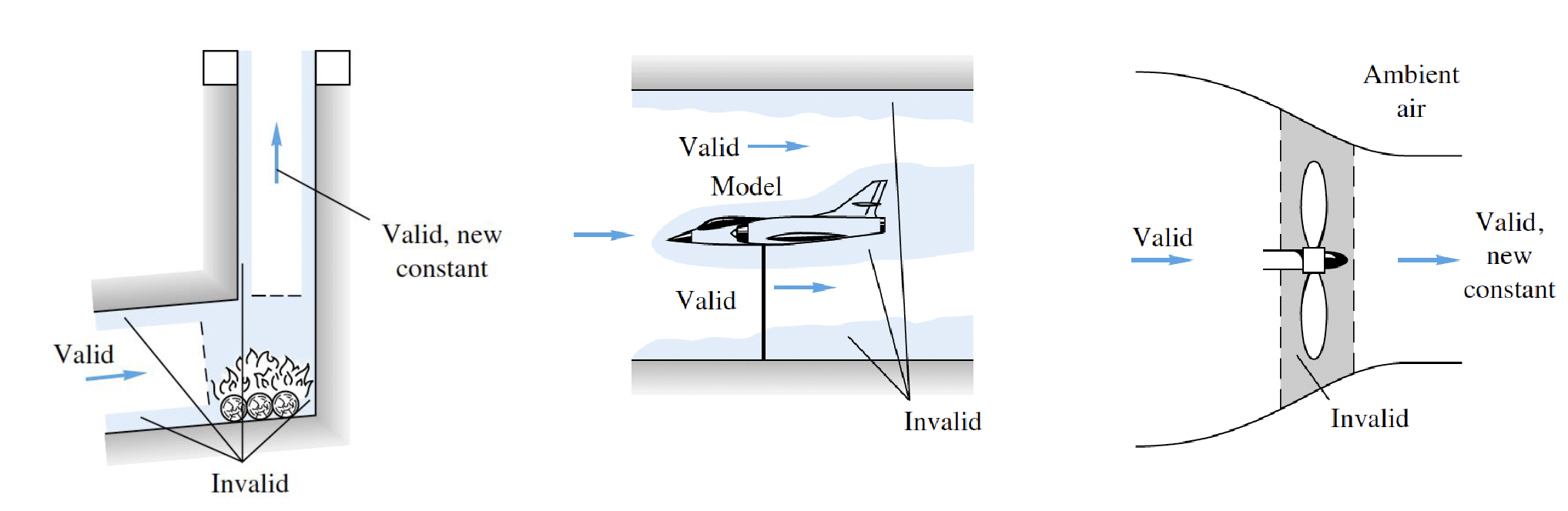
You cant use Bernoulli’s when there is mixing of streams or things that could affect the Bernoulli constant.

For things that are steady, with constant density… we can use Bernoulli’s equation which is…
$\frac{v_1^2}{2}+\frac{p_1}{\rho }+g{z}_1=\frac{v_2^2}{2}+\frac{p_2}{\rho }+g{z}_2$ Where each side of the Bernoulli’s equation is a constant

Main Assumptions

1. Steady flow
2. Incompressible flow - acceptable if the flow mach number is < 0.3
3. Frictionless flow - solid walls introduce friction effects
4. Flow with a single streamline - different streamlines may have different Bernoulli constants based on flow conditions
5. No shaft work between points
6. No heat transfer between points

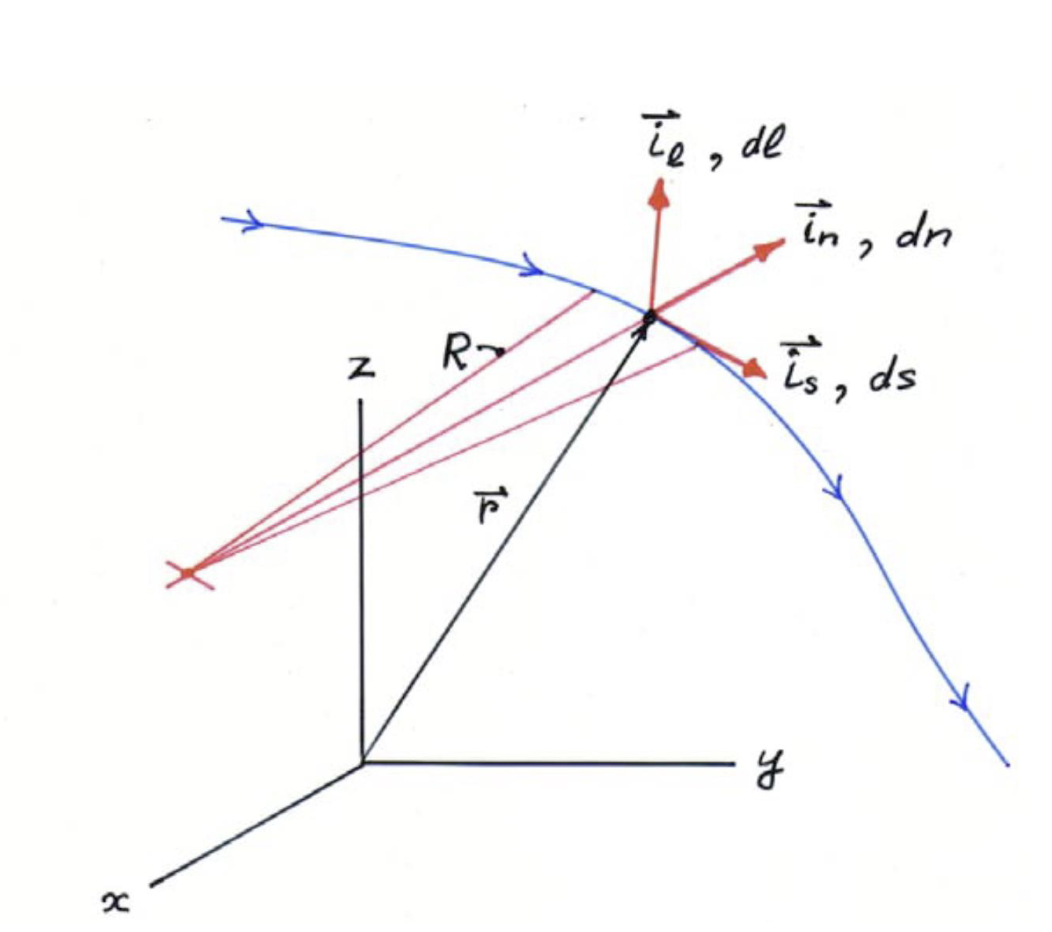
With a Streamline Curve

The streamline coordinates are in the (s, n, l) directions…

• Velocity is tangent to the streamline so using vector notation $V=V{i}_s$
• From this idea, we can derive an expression for acceleration…
• $\left(V\cdot \nabla \right)V=V\frac{\partial }{\partial s}\left(V{i}_s\right)=i_s\frac{\partial }{\partial s}\left(\frac{V^2}{2}\right)+V^2\frac{\partial i_s}{\partial s}$
• Where the first term is the tangential acceleration and the second term is the normal acceleration, this breaks the streamline into a streamline component and a direction change component
• This is a general equation of convective acceleration without specifying what the curvature is

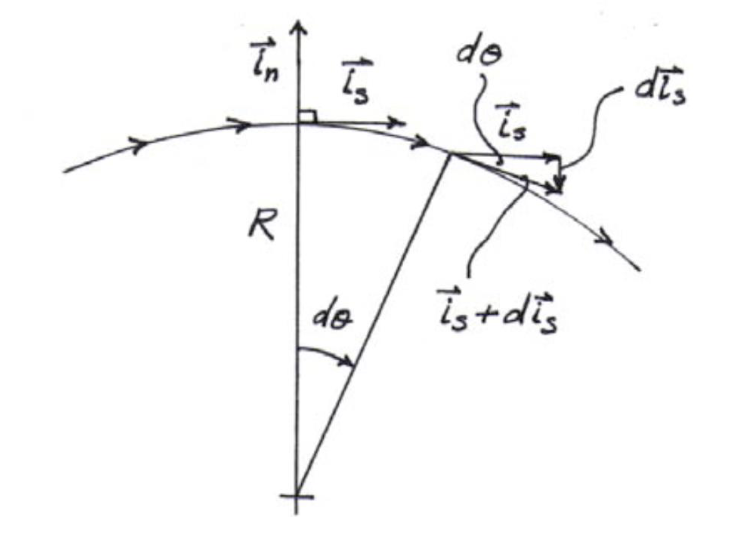
Looking at the normal direction, $d{i}_s=-i_{n}d\theta =-i_n\frac{ds}{R}$…

Using that definition, our acceleration term becomes…

• $\left(V\cdot \nabla V\right)V=i_s\frac{\partial }{\partial s}\left(\frac{V^2}{2}\right)-i_n\frac{V^2}{R}$
• Here, you explicitly know that streamlines are curved and want to describe acceleration in terms of the radius of curvature R

In these two expressions, if there is a gravity term, we would just add a general gravity component term $\frac{d}{ds}\left(gz\right)$ and $\frac{d}{dn}\left(gz\right)$ to our acceleration expression

Note that $\frac{d}{ds}\left(\frac{1}{2}{V}^2+\frac{p}{\rho }+gz\right)=0$ which means our Bernoulli expression is constant along a streamline.

Losses

• Energy can be lost due to mixing and/or friction (dissipated into heat)
• On any specific streamline loss can be –ve or +ve
• But on average losses are positive Use mass and momentum conservation as well as the general Bernoulli equation you can form an expression of the form $\text{V2 p2 term}=\text{V1 p1 term}-\text{something that is always positive which is the loss}$ like this…

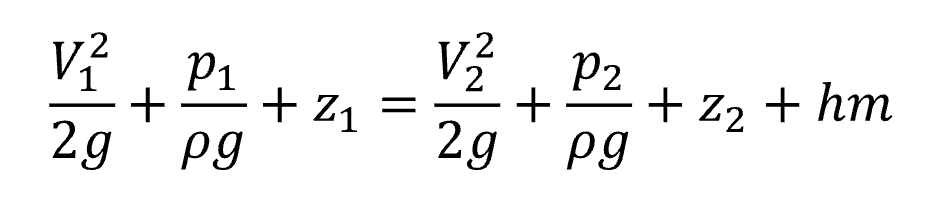
Here, the m indicates minor loss
$k=\frac{h_m}{V^{2}2g}$

General Expression

• $\frac{V_1^2}{2g}+\frac{p_1}{\rho g}+z_1=\frac{V_2^2}{2g}+\frac{p_2}{\rho g}+z_2+h_m+h_f+h_s$
• $h_m$: minor losses: +ve
• $h_f$: friction +ve
• $h_s$: shaft work +ve or -ve

Here, the losses are added in series depending on the pipe connections (ex. for a valve, we would have $\Sigma h=h_{f1}+h_m+h_{f2}$ where the frictional losses are from two pipes and the minor loss is from the valve…)